Normalparabel (nach oben oder unten geöffnet) und zwei Kurvenpunkte gegeben
Nun liegt ein sogenanntes Gleichungssystem vor. In anderen Worten:Man hat nun zwei Gleichungen mit den beiden Unbekannten b und c. Da beide Gleichungen zugleich erfüllt sein müssen, sind die beiden Gleichungen durch die logische Verknüpfung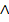 
(UND ZUGLEICH) zu einem Gleichungssystem verbunden. Schüler der Realschule sollten das Zeichen 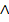besser immer vor die Gleichung II schreiben, da ein Weglassen von manchen Lehrern als Fehler gewertet wird. Schüler anderer Schularten können das Zeichen 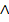einfach weglassen;besonders im Gymnasium wird das nicht so eng gesehen. Sicherheitshalber vergleichst du mit Aufgaben, die dein Schullehrer selbst vorgeführt hat, und schaust, wie er es geschrieben hat.
Das Gleichungssystem kann dann entweder mit dem Einsetzungsverfahren oder dem Additionsverfahren gelöst werden, das ist Geschmackssache und hängt von den vorkommenden Zahlen ab. Die meisten Schüler bevorzugen zwar das Einsetzungsverfahren, weil sie es besser beherrschen. Generell ist jedoch das Additionsverfahren weniger aufwändig und daher zu empfehlen.
Kurzwiederholung des Einsetzungsverfahrens:
Eine der beiden Gleichungen (z.B. I) wird nach einer der beiden Unbekannten (z.B. nach c) aufgelöst und in die andere Gleichung eingesetzt. Dadurch erhält man eine Gleichung, die nur noch die zweite Unbekannte (z.B. b) enthält. Nun kann b durch Umstellen dieser Gleichung berechnet werden. Ist b bekannt, setzt man b in eine der beiden Gleichungen I oder II ein. Ebenfalls durch Umstellen kann nun die verbliebene Unbekannte c ermittelt werden.
Kurzwiederholung des Additionsverfahrens:
Die beiden Gleichungen I und II werden falls nötig so mit Faktoren (Zahlen) multipliziert, dass sich vor einer der beiden Unbekannten in beiden Gleichungen, vom Vorzeichen einmal abgesehen, die gleichen Zahlen ergeben. Beim Aufstellen von Parabeln entfällt dieser Schritt, da bereits in beiden Gleichungen jeweils c, also +1c vorkommt. Die Gleichungen werden dann voneinander abgezogen (oder addiert), so dass eine Unbekannte wegfällt. Beim Aufstellen von Parabelgleichungen fällt bei der Subtraktion der Gleichungen I und II immer die Unbekannte c heraus, so dass sich b leicht durch Umstellen berechnen lässt. Dann wird b in eine der beiden Gleichungen I oder II eingesetzt. Dadurch entsteht eine Gleichung, die nur noch b enthält. Nun kann wiederum durch Umstellen c ermittelt werden.
Nun sind b und c berechnet. Sie müssen nur noch in den allgemeinen Ansatz der Parabel eingesetzt werden und man hat die gesuchte Funktionsgleichung der Parabel aufgestellt.
