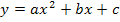Ein Koeffizient (a, b oder c) und zwei Kurvenpunkte gegeben

(Genauere Erläuterungen zu diesem Verfahren findest du im Bereich Algebra im Kapitel Gleichungssysteme:Zwei Gleichungen für zwei Unbekannte/Additionsverfahren)

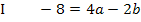
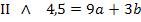
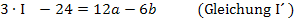
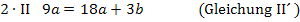
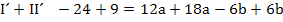
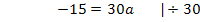
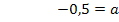
Nun ist die erste Unbekannte a ermittelt. Um die verbleibende Unbekannte b berechnen zu können, setzt man den soeben ermittelten Wert für a in Gleichung I oder II ein. In welche der beiden Gleichungen eingesetzt wird, ist hier Geschmackssache. Allgemein verwendet man natürlich diejenige Gleichung, die die einfacheren Zahlen enthält. Wir setzten nun a in I.

a in I:

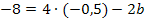
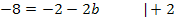
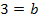
Egal welches Verfahren verwendet wird, es ergeben sich selbstverständlich die selben Ergebnisse für a und b: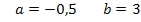

Diese Werte müssen nur noch in den allgemeinen Ansatz der Parabel 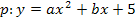eingesetzt werden.

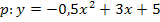
Nun ist die Gleichung der Parabel p ermittelt.

Zusammenfassung: Gesucht: Gleichung einer Parabel mit zwei gegeben Kurvenpunkten A und B sowie einem Koeffizienten a, b oder c Lösung: · Allgemeiner Ansatz: · Gegebenen Koeffizienten a, b oder c falls nötig in den allgemeinen Ansatz einsetzen · Koordinaten des ersten Kurvenpunkts A für x bzw. y in den allgemeinen Ansatz einsetzen · Koordinaten des zweiten Kurvenpunkts B für x bzw. y in den allgemeinen Ansatz einsetzen · Es liegt nun ein Gleichungssystem mit zwei Gleichungen für zwei Unbekannte vor · Gleichungssystem mit Einsetzungs- oder Additionsverfahren lösen · Berechnete Koeffizienten in den allgemeinen Ansatz einsetzen

---