Ein Koeffizient (a, b oder c) und zwei Kurvenpunkte gegeben
B(3|9,5) einsetzen in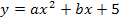 
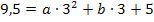
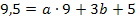
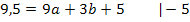
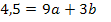(Gleichung II)
Da beide Punkte auf der Parabel liegen sollen, müssen die Gleichungen I und II beide zugleich erfüllt sein. Mathematisch ausgedrückt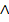:I 
II
Anmerkung:Das Zeichen 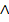bedeutet UND-ZUGLEICH.
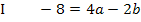
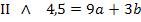
Es liegt nun ein Gleichungssystem mit zwei Gleichungen für die beiden Unbekannten a und b vor. Es kann wahlweise mit dem Einsetzungs- oder mit dem Additionsverfahren gelöst werden. Es werden im Folgenden beide Methoden vorgeführt. So kannst du dir leichter aussuchen, welches Verfahren dir persönlich besser liegt.
1. Methode: Einsetzungsverfahren
Eine der beiden Gleichungen muss nach einer der beiden Unbekannten a oder b aufgelöst werden und dann in die andere Gleichung eingesetzt werden. In diesem Fall lässt sich die Gleichung I gut nach b auflösen. Das Ergebnis setzen wir dann für b in II ein. So erhält man eine Gleichung, die nur noch a enthält. Damit kann a leicht berechnet werden.
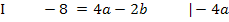
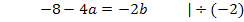
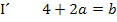
I´in II:
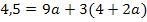
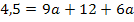
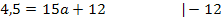
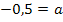
Nun ist die erste Unbekannte a ermittelt. Um auch die zweite Unbekannte b zu berechnen, setzen wir den soeben berechneten Wert für a in Gleichung I´ein. (Man könnte a ebenso in I oder II einsetzen. Das führt zum selben Ergebnis für b, ist jedoch umständlicher, da man erst noch nach b auflösen müsste.)
a in I´:
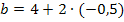
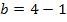
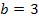
2. Methode:Additionsverfahren
Hier noch einmal das Gleichungssystem, das zu lösen ist:
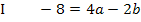
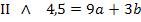
Leider steht weder vor a in beiden Gleichungen die selbe Zahl, noch vor b, so dass durch eine sofortige Addition bzw. Subtraktion der beiden Gleichungen keine der Unbekannten wegfallen würde. Wir müssen daher erst die beiden Gleichungen so mit bestimmten Zahlen multiplizieren, dass vor einer der beiden Unbekannten, vom Vorzeichen einmal abgesehen, die gleiche Zahl zu stehen kommt. Da hier vor b die etwas angenehmeren Zahlen stehen, entscheiden wir uns dafür, die Gleichungen so mit Faktoren zu multiplizieren, dass vor b die (vom Vorzeichen abgesehen) gleichen Zahlen entstehen. Zuerst multiplizieren wir dazu die gesamte Gleichung I mit dem Faktor 3 und die gesamte Gleichung II mit dem Faktor 2. Die neuen Gleichungen werden mit I´und II´bezeichnet. Dadurch steht in den Gleichungen I´und II´jeweils die Zahl 6 vor b (genau genommen steht dann in I´-6b und in II´+6b). Addiert man nun die Gleichungen I´und II´, fällt die Unbekannte b weg. Es liegt nun eine Gleichung vor, die als einzige Unbekannte a enthält. Daher kann a jetzt leicht durch Umstellen der Gleichung ermittelt werden.
