Drei Kurvenpunkte gegeben
Danach lässt sich a leicht ausrechnen.
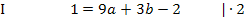
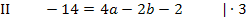
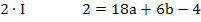
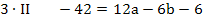
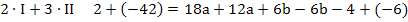
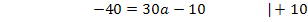
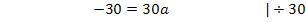
Nun kann der soeben berechnete Wert für a in Gleichung I oder II eingesetzt werden. Wir setzen hier a in I ein.
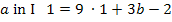
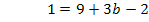
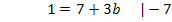
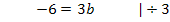
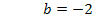
Anmerkung:An Stelle des Additionsverfahrens hätte natürlich auch das Einsetzungsverfahren verwendet werden können. Man hätte beispielsweise Gleichung II nach b auflösen können und dann den entstandenen Term für b in Gleichung I einsetzen können.
Nun sind alle Koeffizienten a, b und c berechnet: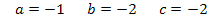 
Sie müssen nur noch in den allgemeinen Ansatz der Parabel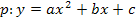 
eingesetzt werden. So erhalten wir die gesuchte Gleichung der Parabel p.
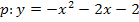
2. Bsp.: Ermittle die Gleichung einer Parabel p, die durch die Punkte A(-1|-3),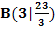 
und C(2|4) verläuft!
Lösung:
Wir verwenden den allgemeinen Ansatz für eine Parabel 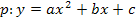und setzen der Reihe nach die Koordinaten der Punkte A, B und C für x bzw. y ein.
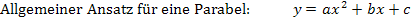
Nun müssen wir das Gleichungssystem, bestehend aus den Gleichungen I, II und III lösen. Wir wählen das Additionsverfahren.
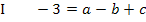
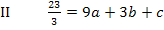
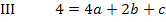
Es bietet sich an zuerst zwei Gleichungen herzustellen, die nur noch die beiden Unbekannten a und b enthalten, da sich c leicht durch Subtraktion zweier Gleichungen eliminieren lässt. Wir brauchen später zwei Gleichungen, die jeweils nur noch a und b enthalten, um die beiden Unbekannten a und b berechnen zu können. Man benötigt schließlich immer so viele Gleichungen, wie man Unbekannte hat, um diese Unbekannten zu berechnen. Daher subtrahieren wir von Gleichung II die Gleichung I und nachher von Gleichung III die Gleichung I. (Man hätte auch jeweils zwei andere Gleichungen voneinander abziehen können. Die Unbekannte c fällt auf jeden Fall heraus und das ist ja unser Ziel.)
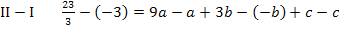
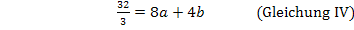
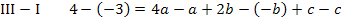
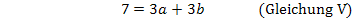
Die Gleichungen IV und V bilden zusammen ein Gleichungssystem, bestehend aus zwei Gleichungen für die zwei Unbekannten a und b. Wir wenden noch einmal das Additionsverfahren an. Gleichung IV wird zuerst mit dem Faktor 3 und Gleichung V mit dem Faktor 4 multipliziert, damit nachher durch Subtraktion der entstandenen Gleichungen die Unbekannte b wegfällt. Dann kann endlich a berechnet werden.
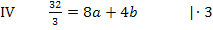
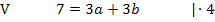
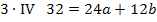
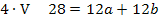
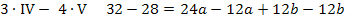
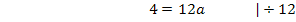
Nun ist die erste Unbekannte a ermittelt. Sie kann beispielsweise in Gleichung V eingesetzt werden. So lässt sich b berechnen.
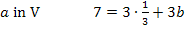
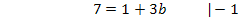
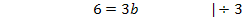
Um die letzte Unbekannte c berechnen zu können, setzt man die soeben ermittelten Werte für a und b in Gleichung I ein. (Man hätte a und b auch II oder III einsetzen können, doch ist in diesem Beispiel Gleichung I am einfachsten.
