Drei Kurvenpunkte gegeben
) Hat allerdings keiner der gegebenen Kurvenpunkte die x-Koordinate x = 0, wird es deutlich schwieriger a, b und c zu berechnen und somit die Parabelgleichung zu finden.
Nachdem man die Koordinaten der drei Kurvenpunkte eingesetzt hat, muss das entstandene Gleichungssystem gelöst werden. Dazu stehen verschiedene Lösungsverfahren zu Wahl:Das Einsetzungsverfahren, das Additionsverfahren oder das Determinantenverfahren. Letzteres steht leider seit der Einführung des G8 nicht mehr auf dem Lehrplan der bayerischen Gymnasien. Auch in der FOS oder BOS wird das Determinantenverfahren meist nicht unterrichtet, obwohl es wohl das einfachste der genannten Lösungsverfahren ist. (Es ist vermutlich zu einfach. Das könnte ja jeder Schüler ohne Probleme lernen!) Wir müssen uns daher mit dem Einsetzungs- oder Additionsverfahren an die Aufgabe machen, mit den drei Gleichungen die drei Unbekannten a, b und c zu berechnen.
Schüler, die das Determinantenverfahren in der Schule jedoch gelernt haben, können natürlich auch diese Methode verwenden. Wie die einzelnen Verfahren funktionieren, wird im Bereich Algebra im Kapitel Gleichungssysteme:Drei Gleichungen für drei Unbekannte ausführlich erklärt. Auf jeden Fall solltest du Gleichungssysteme mit nur zwei Gleichungen und zwei Unbekannten gut lösen können. Das ist absolute Grundvoraussetzung für die folgenden Aufgaben! Wiederhole ansonsten zuerst das Kapitel Gleichungssysteme:Zwei Gleichungen für zwei Unbekannte ausführlich, bevor du dich an Gleichungssysteme mit drei Gleichungen heran wagst!
Nun folgen zwei Beispiele, wobei das 1. Bsp. noch relativ leicht ist, da es den Sonderfall, dass einer der Kurvenpunkte die x-Koordinate x = 0 besitzt, zeigt. Es führt daher nur zu einem Gleichungssystem mit zwei Gleichungen für zwei Unbekannte. Das 2. Bsp. stellt dann den Regelfall dar, dass also keiner der drei gegebenen Kurvenpunkte die x-Koordinate x = 0 besitzt. Es führt daher zu einem Gleichungssystem mit drei Gleichungen für drei Unbekannte.
1. Bsp.:Die Punkte A(0|-2), B(3|1) und C(-2|-14) liegen auf der Parabel p. Ermittle die Gleichung der Parabel p!
Lösung:
Der Punkt A hat die x-Koordinate x = 0. Daher setzen wir diesen Punkt als ersten ein. So erhalten wir direkt den Koeffizienten c.
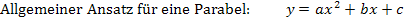


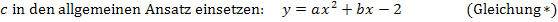
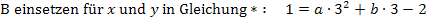
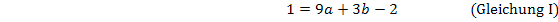
![]()
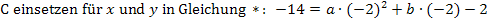
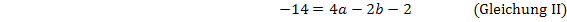
![]()
Nun müssen wir das Gleichungssystem, bestehend aus den Gleichungen I und II lösen. Wir wählen das Additionsverfahren. Um b zu eliminieren, multiplizieren wir Gleichung I mit dem Faktor 2, Gleichung II mit dem Faktor 3 und addieren die so entstandenen Gleichungen.

