Beide Nullstellen und ein weiterer Kurvenpunkt oder ein Koeffizient a, b oder c gegeben
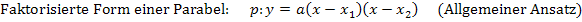
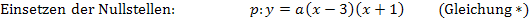
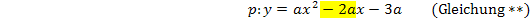
Der Koeffizient b = -4 entspricht dem Ausdruck, der in Gleichung ** vor x steht (gelb unterlegt), also dem Ausdruck -2a. Daher kann der Ausdruck -2a mit dem für b gegebenen Wert -4 gleichgesetzt werden. So erhält man durch Koeffizientenvergleich:
| 
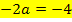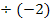
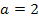
Nun kann man den soeben berechneten Wert für a in Gleichung * einsetzen. Dann liegt die Parabel p in ihrer faktorisierten Form vor. Durch Ausmultiplizieren und Zusammenfassen erhält man die gewünschte Form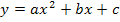 
. Daraus kann c direkt abgelesen werden. Schneller kommen wir allerdings zum gewünschten Ergebnis, wenn wir a in Gleichung ** einsetzen und die dadurch entstandene Gleichung soweit möglich vereinfachen. Dies wird im Folgenden vorgeführt.
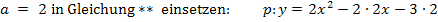
Die Parabel liegt nun in der gewünschte Form 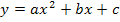vor, wobei für die Koeffizienten gilt: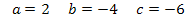 
Dass sich, wie in der Aufgabenstellung bereits gegeben, für b der Wert -4 ergibt, dient zur Kontrolle der Rechnung. Erhältst du für b einen anderen Wert als in der Angabe genannt, weißt du, dass du dich verrechnet hast.
Hinweis:Solltest du mit diesem Verfahren gar nicht zurechtkommen, besteht außerdem die Möglichkeit, die Aufgabe mit einer ganz anderen Methode zu lösen:Man kann die Nullstellen auch als zwei normale Kurvenpunkte ansehen. Dann verwendet man das Verfahren, das bei Zwei Kurvenpunkte und ein Koeffizient gegeben erläutert ist. Diese Methode ist aber wesentlich aufwändiger und daher eigentlich schwieriger.
2. Bsp.: Von einer Parabel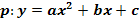 
mit 
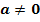sind die Nullstellen 
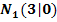und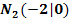 
bekannt. Berechne die Koeffizienten a und b, wenn c = -1,5 ist!
Lösung:
Da beide Nullstellen gegeben sind, verwenden wir wieder die faktorisierte Form einer Parabel als allgemeinen Ansatz.
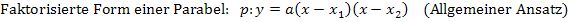
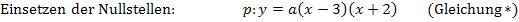
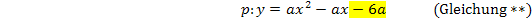
Der Koeffizient c = -1,5 entspricht dem Ausdruck in Gleichung **, der kein x enthält (gelb unterlegt), also dem Ausdruck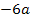 
. Daher kann der Ausdruck 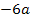mit dem für c angegebenen Wert -1,5 gleichgesetzt werden. So erhält man durch Koeffizientenvergleich:
| 
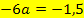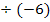
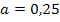
Nun kann man den soeben berechneten Wert für a in Gleichung * einsetzen. Dann liegt die Parabel p in ihrer faktorisierten Form vor. Durch Ausmultiplizieren und Zusammenfassen erhält man die gewünschte Form 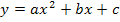. Daraus kann der noch nicht berechnete Koeffizient b direkt abgelesen werden. Schneller kommen wir allerdings zum gewünschten Ergebnis, wenn wir a in Gleichung ** einsetzen und die dadurch entstandene Gleichung soweit möglich vereinfachen. Im Folgenden wird diese Methode gezeigt.
