Beide Nullstellen und ein weiterer Kurvenpunkt oder ein Koeffizient a, b oder c gegeben
2. Beide Nullstellen und einer der Koeffizienten a, b oder c bekannt
Die faktorisierte Form hilft immer weiter, wenn beide Nullstellen der Parabel bekannt sind. An Stelle des zusätzlichen Kurvenpunktes kann jedoch auch einer der Koeffizienten a, b oder c gegeben sein.
Besonders einfach lässt sich die Funktionsgleichung einer Parabel ermitteln, wenn der Öffnungsfaktor a zusätzlich zu den Nullstellen bekannt ist. Dann können a und die x-Koordinaten der Nullstellen jeweils direkt in den allgemeinen Ansatz der faktorisierten Form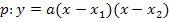 
eingesetzt werden. Man muss nur noch ausmultiplizieren und soweit möglich zusammenfassen. Schon ist man fertig.
Deutlich schwieriger ist es mit Hilfe eines gegebenen Koeffizienten b oder c und den beiden Nullstellen die Parabelgleichung zu finden. Zuerst setzt man die x-Koordinaten der beiden Nullstellen jeweils für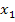 
und 
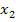in den allgemeinen Ansatz der faktorisierten Form der Parabel 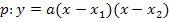ein. Man erhält eine Gleichung, die noch x, y und a enthält. Nun wird die rechte Seite dieser Gleichung ausmultipliziert und soweit möglich vereinfacht. Dabei wird, wie gewöhnlich, nach absteigender x-Potenz geordnet. Der Ausdruck, der nun vor x steht (er enthält den momentan noch unbekannten Koeffizienten a), entspricht dabei b. Der hinterste Ausdruck ganz ohne x entspricht c. Ist nun beispielsweise b gegeben, nimmt man den Ausdruck, der vor x steht, und setzt ihn mit dem gegebenen Wert von b gleich. (Ist c angegeben, setzt man entsprechend den Ausdruck ohne x mit dem für c angegebenen Wert gleich.) Dieses Vorgehen wird übrigens als Koeffizientenvergleich bezeichnet. Man erhält dadurch eine Gleichung, die als einzige Unbekannte a enthält, so dass jetzt a leicht berechnet werden kann. Nun können der soeben berechnete Wert für a und die x-Koordinaten der Nullstellen wieder in den allgemeinen Ansatz der faktorisierten Form eingesetzt werden. Man muss noch ausmultiplizieren und soweit möglich zusammenfassen, dann ist man endlich fertig.
Sollte dir das Vorgehen noch nicht ganz klar sein, ist das nicht weiter schlimm. Es ist schließlich wirklich nicht ganz einfach. Im Folgenden findest du jeweils ein konkretes Beispiel, wie mit zwei Nullstellen und b oder c eine Parabelgleichung am geschicktesten ermittelt wird. Studiere die Beispiele genau! Danach müsste dir das Verfahren klar sein.
1. Bsp.: Von einer Parabel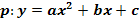 
mit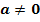 
sind die Nullstellen 
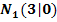und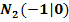 
bekannt. Berechne die Koeffizienten a und c, wenn b = -4 ist!
Lösung:
Da beide Nullstellen gegeben sind, verwenden wir die faktorisierte Form einer Parabel als allgemeinen Ansatz.
