Beide Nullstellen und ein weiterer Kurvenpunkt oder ein Koeffizient a, b oder c gegeben
Nun hast du die Parabel in faktorisierter Form vorliegen und musst sie nur noch, wie bereits oben beschrieben, vereinfachen, um die verlangte Form 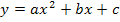 zu erhalten. Ein konkretes Beispiel für diesen Aufgabentyp findest du etwas weiter unten. (Vergleiche Bsp. 1!)
zu erhalten. Ein konkretes Beispiel für diesen Aufgabentyp findest du etwas weiter unten. (Vergleiche Bsp. 1!)
Achtung: Die meisten Schüler versuchen gerne diese Aufgabenstellung direkt mit der Form 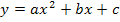 zu lösen. Meist wird versucht, die gegebenen beiden Nullstellen und den zusätzlich bekannten Kurvenpunkt für x bzw. y in den Ansatz
zu lösen. Meist wird versucht, die gegebenen beiden Nullstellen und den zusätzlich bekannten Kurvenpunkt für x bzw. y in den Ansatz 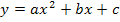 einzusetzen. Das ergibt dann ein Gleichungssystem mit drei Gleichungen und den drei Unbekannten a, b und c. So ein Gleichungssystem ist jedoch meist nur mit extrem großen Rechenaufwand zu lösen. Daher ist von dieser Methode wirklich eindeutig abzuraten! Viel schneller und natürlich auch einfacher geht es doch mit der faktorisierten Form!
einzusetzen. Das ergibt dann ein Gleichungssystem mit drei Gleichungen und den drei Unbekannten a, b und c. So ein Gleichungssystem ist jedoch meist nur mit extrem großen Rechenaufwand zu lösen. Daher ist von dieser Methode wirklich eindeutig abzuraten! Viel schneller und natürlich auch einfacher geht es doch mit der faktorisierten Form!
Merke:
Sind beide Nullstellen einer Parabel bekannt, nicht mit der Form 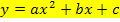 als allgemeinen Ansatz nehmen, sondern immer die faktorisierte Form
als allgemeinen Ansatz nehmen, sondern immer die faktorisierte Form 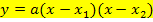 verwenden!
verwenden!
Bsp.: Eine Parabel p hat die Nullstellen 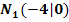 und
und 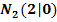 . Die Parabel verläuft außerdem durch den Punkt A(-6|-8). Ermittle die Gleichung der Parabel p in der Form
. Die Parabel verläuft außerdem durch den Punkt A(-6|-8). Ermittle die Gleichung der Parabel p in der Form 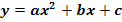 !
!
Lösung:
Da beide Nullstellen gegeben sind, verwenden wir die faktorisierte Form einer Parabel als allgemeinen Ansatz.
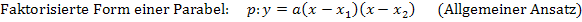
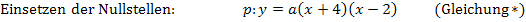

![]()
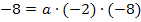
![]()
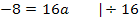
![]()
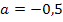
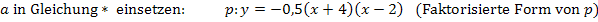
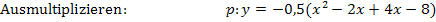


Nun liegt die Parabel in der Form 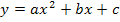 vor.
vor.
Hinweis:Solltest du mit diesem Verfahren gar nicht zurechtkommen, besteht außerdem die Möglichkeit, die Aufgabe mit einer ganz anderen Methode zu lösen:Man kann die Nullstellen auch als zwei normale Kurvenpunkte ansehen. Mit dem zusätzlich angegeben Kurvenpunkt hat man also drei Punkte gegeben, die auf der Parabel liegen. Man kann daher auch das Verfahren anwenden, das bei Drei Kurvenpunkte gegeben erläutert ist. Diese Methode ist aber wesentlich aufwändiger und schwieriger, weil dabei ein Gleichungssystem mit drei Gleichungen und drei Unbekannten zu lösen ist. Wenn beide Nullstellen und ein weiterer Kurvenpunkt gegeben sind, ist von dieser Methode im Allgemeinen absolut abzuraten! Es dauert einfach viel zu lange und führt, im Vergleich zum oben gezeigten Rechenweg, viel öfter zu Rechenfehlern.
| Zusammenfassung:
Gesucht: Gleichung einer Parabel mit zwei gegeben Nullstellen und einem Kurvenpunkt A · Allgemeiner Ansatz: · x-Koordinaten der Nullstellen für für · Koordinaten von Kurvenpunkt A für x und y einsetzen · nach a auflösen: · a einsetzen in Gleichung *: · Faktorisierte Form der Parabel ausmultiplizieren |

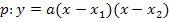
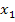 bzw.
bzw. 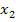 einsetzen:
einsetzen:  Gleichung *
Gleichung *