Funktionsgleichung einer Parabel aufstellen
Die Gleichung einer Parabel p lautet in der allgemeinen Form bekanntlich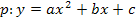 
. Nur eine andere Schreibweise dafür ist 
.
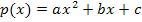Zur Erinnerung: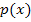 
(sprich „ p von x“) ist gleichbedeutend mit y. In diesem Fall ist p die Bezeichnung für die Parabel;sie kann aber auch eine andere Bezeichnung haben, wie zum Beispiel 
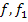oder 
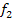. Das kommt auf die Benennung in der Aufgabenstellung an. Entsprechend gilt dann 
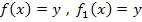oder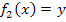 
.
Soll die Funktionsgleichung einer Parabel ermittelt werden, müssen die Koeffizienten a, b und c, also die Zahlen vor 
, vor x und die Zahl ohne x, berechnet werden.
Dafür kommen verschiedene Rechenwege in Frage, je nach dem, was gegeben ist. So können beispielsweise einer der Koeffizienten a, b oder c und zwei Punkte A und B der Parabel gegeben sein. Damit lässt sich die Funktionsgleichung noch relativ einfach durch ein Gleichungssystem mit zwei Gleichungen für zwei Unbekannte ermitteln. Genaueres dazu siehe unten!
Ist der Scheitelpunkt der Parabel und ein weiterer Kurvenpunkt P gegeben, lässt sich mit Hilfe der Scheitelform die Parabelgleichung besonders schnell aufstellen.
Merke:Immer wenn der Scheitel der Parabel bekannt ist, verwendet man als Ansatz die Scheitelform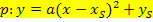 
, um letztendlich a, b und c zu berechnen!
Ist keiner der drei Koeffizienten a, b oder c bekannt, lässt sich mit Hilfe dreier beliebiger Kurvenpunkte, die Gleichung der Parabel ermitteln. Dieser Fall ist meist mit deutlich mehr Rechenaufwand verbunden, da ein Gleichungssystem mit drei Gleichungen für die drei Unbekannten a, b und c gelöst werden muss. Mit drei Punkten eine Parabelgleichung aufzustellen, wird nur von Gymnasiasten oder Schülern der FOS bzw. BOS verlangt, nicht aber von Realschülern.
| Mit den folgenden Angaben kann die Gleichung einer Parabel aufgestellt werden.
·Normalparabel (nach oben oder unten geöffnet) und zwei Kurvenpunkte gegeben ·Normalparabel (nach oben oder unten geöffnet) und Scheitelpunkt S gegeben ·Öffnungsfaktor a und Scheitelpunkt S gegeben ·Scheitel und ein weiterer Kurvenpunkt gegeben ·Ein Koeffizient (a, b oder c) und zwei Kurvenpunkte gegeben ·Beide Nullstellen und ein weiterer Kurvenpunkt oder ein Koeffizient a, b oder c gegeben ·Drei Kurvenpunkte gegeben (Nicht für Realschüler!) |
