Faktorisierte Form (Produktform) einer quadratischen Funktion
Sollte es sich bei dem zu faktorisierenden Term um eine erste oder zweite binomische Formelhandeln, die du jedoch nicht erkannt hast, kann die oben beschriebene Methode trotzdem angewendet werden:Es werden sich dann allerdings für 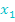 und
und 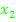 durch die Mitternachtsformelzweimal dieselben Werte ergeben:
durch die Mitternachtsformelzweimal dieselben Werte ergeben: 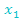 =
= 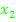 =
= 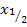 Du musst sie beide in die Formel
Du musst sie beide in die Formel 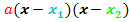 einsetzen, so als wären es zwei verschiedene Zahlen. Du bekommst dadurch zweimal die gleiche Klammer, die sich durch ein Quadrat zusammenfassen lässt. Das ist immer dann der Fall, wenn der Scheitel der Parabel auf der x-Achse liegt, also wenn für die y-Koordinate des Scheitels gilt
einsetzen, so als wären es zwei verschiedene Zahlen. Du bekommst dadurch zweimal die gleiche Klammer, die sich durch ein Quadrat zusammenfassen lässt. Das ist immer dann der Fall, wenn der Scheitel der Parabel auf der x-Achse liegt, also wenn für die y-Koordinate des Scheitels gilt 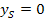 . Dann entspricht die x-Koordinate des Scheitels
. Dann entspricht die x-Koordinate des Scheitels 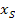 der einzigen Nullstelle
der einzigen Nullstelle 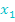 =
= 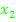 =
= 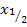 .
.
2. Bsp.: 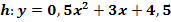
Die Funktion 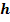 soll faktorisiert, also vollständig in Linearfaktoren zerlegt werden.
soll faktorisiert, also vollständig in Linearfaktoren zerlegt werden.
Lösung:
Wenn man zuerst die Zahl 0,5 ausklammert, wird die erste binomische Formel![]()
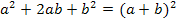 erkennbar.
erkennbar.
Zur Erinnerung:Man klammert die Zahl 0,5 aus, indem man durch 0,5 bzw. 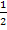 teilt. Durch einen Bruch teilt man, indem man mit dem Kehrwert multipliziert, also in diesem Fall mit
teilt. Durch einen Bruch teilt man, indem man mit dem Kehrwert multipliziert, also in diesem Fall mit 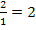 multipliziert.
multipliziert.
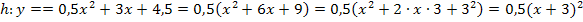
So kann man diese Funktion eigentlich am geschicktesten faktorisieren. Wenn du aber mit den binomischen Formeln auf Kriegsfußstehst, kannst du stattdessen, wie bereits erwähnt, auch die oben beschriebene Faktorisierungs-Methode anwenden:
 (Gleich Null setzen, um die Nullstellen zu berechnen)
(Gleich Null setzen, um die Nullstellen zu berechnen)
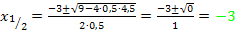 (Mitternachtsformel)
(Mitternachtsformel)
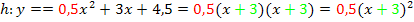 (Faktorisierung)
(Faktorisierung)
Wir erhalten natürlich wieder dasselbe Ergebnis wie vorher, als wir die binomische Formel verwendeten.
| Übersicht über die Möglichkeiten beim Faktorisieren:
· Ausklammern (falls möglich) · Eine der Binomischen Formeln anwenden (falls möglich) · Funktion gleich Null setzen und Mitternachtsformel anwenden Dann zum Faktorisieren die Zahl vor So ergibt sich: Ist bei der Mitternachtsformel die Diskriminante (der Ausdruck unter der Wurzel) negativ, gibt es keine Nullstellen. Die Funktion kann nicht faktorisiert werden. |
- Page 4 of 4
- « Previous
- 1
- 2
- 3
- 4
- Next »

 Nullstellen
Nullstellen 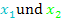
 abschreiben und mit den beiden Klammern multiplizieren;in den Klammern steht jeweils x und dahinter eine der Nullstellen, aber mit umgedrehtem Vorzeichen.
abschreiben und mit den beiden Klammern multiplizieren;in den Klammern steht jeweils x und dahinter eine der Nullstellen, aber mit umgedrehtem Vorzeichen.
