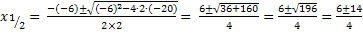Faktorisierte Form (Produktform) einer quadratischen Funktion
Einfacher ist jedoch die Anwendung der folgenden Methode:
· Gleich Null setzen: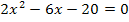 
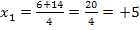
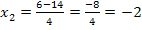
· Faktorisierung: f(x) =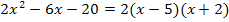 
Nun ist die Funktion vollständig faktorisiert: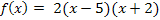 
Dass die Umformung richtig ist, kannst du ganz einfach nachprüfen, indem du die faktorisierte Form ausmultiplizierst;es wird wieder die allgemeine Form herauskommen! Außerdem haben wir oben gelernt, dass die Nullstellen aus der faktorisierten Form abgelesen werden können, indem man bei den Zahlen in den Klammern jeweils die Vorzeichen umdreht. Umgekehrt kann die faktorisierte Form bei bekannten Nullstellen gebildet werden, indem man in den Klammern der faktorisierten Form die Nullstellen jedoch mit umgedrehten Vorzeichen einfügt. Man darf nur nicht vergessen, den Koeffizienten a (d.h. die Zahl, die in der allgemeinen Form vor dem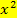 
steht) vor die Klammern zu schreiben.
Ist dir noch nicht wirklich klar, warum die Zerlegung der Funktion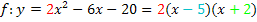 
richtig ist? Dann überlege dir Folgendes:
Die Gleichung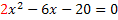 
ist nur für 
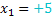und 
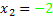erfüllt.(Vergleiche dazu die oben gezeigte Rechnung mit der Mitternachtsformel!)
Die Gleichung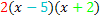 
ist ebenfalls nur für 
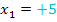und 
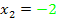erfüllt. Erinnere dich dazu an die Regel:„Ein Produkt ist gleich Null, wenn einer der Faktoren Null ist.“ Die erste Klammer wird Null, wenn man 
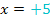setzt;die zweite Klammer wird Null, wenn man 
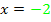setzt. Daher wird das Produkt 
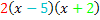gleich Null, wenn 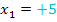oder 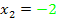gesetzt wird.
Die Gleichungen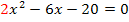 
und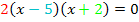 
haben also beide die selben Lösungen. Der Faktor 
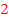ist nötig, damit sich beim Ausmultiplizieren des Terms 
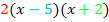wirklich 
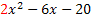ergibt. Die Gleichung 
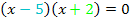hätte zwar auch die selben Lösungen wie die Gleichung 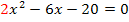nämlich 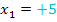und 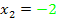. Wenn man 
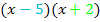ausmultipliziert, ergibt sich jedoch:
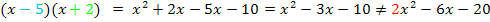
Ohne den Faktor 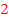erhalten wir also nicht den Term 
!
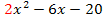Hinweise zum Faktorisieren:
Ein Funktionsterm der Form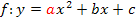 
lässt sich nur dann in der faktorisierten Form 
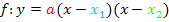schreiben, wenn 
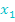und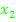 
die Nullstellen der Funktion, also die Lösungen der Gleichung 
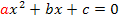sind. Hat die Gleichung keine Lösung, d.h. die Funktion hat keine Nullstellen, so lässt sich der Funktionsterm nicht faktorisieren.
Beim Faktorisieren wird die Zahl a (Zahl vor der höchsten x-Potenz) einfach abgeschrieben und vor die Klammern gesetzt.
In die Klammern der faktorisierten Form schreibt man zuerst x und dann eine der beiden Nullstellen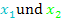 
aber mit umgedrehtem Vorzeichen! Das kommt daher, dass in der Formel 
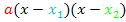ein Minus-Zeichen vor dem 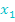und dem 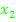steht.
