Faktorisierte Form (Produktform) einer quadratischen Funktion
In diesem Beispiel liegen die Nullstellen daher bei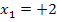 
und 
.
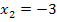Alle Punkte, die auf der x-Achse liegen, müssen die y-Koordinate y = 0 haben. (So berechnet man schließlich auch die Nullstellen.) Die Schnittpunkte der Funktion mit der x-Achse lauten also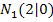 
und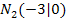 
.
Ist eine Funktion in ihrer faktorisierten Form gegeben und es sollen ihre Nullstellen oder Schnittpunkte mit der x-Achse ermittelt werden, solltest du auf keinen Fall in die allgemeine Form, d.h. in die ausmultiplizierte Form der Funktion, umrechnen! Um mit der ausmultiplizierten Form der Parabel die Nullstellen zu berechnen, bräuchtest du nämlich die Mitternachtsformel (oder die quadratische Ergänzung), was mit einem erheblich größeren Rechenaufwand verbunden wäre. Warum also erst in die viel unpraktischere allgemeine Form umrechnen, wenn es doch mit der faktorisierten Form viel einfacher ist, die Nullstellen zu berechnen!
Umwandlung der faktorisierten Form in die allgemeine Form (a,b,c-Form) der Parabel:
Bei der Berechnung der Nullstellen macht es zwar keinen Sinn, in die allgemeine Form umzurechnen, wenn es aber doch einmal verlangt wird, kannst du die faktorisierte Form in die allgemeine Form (a,b,c-Form) umrechnen, indem du alle Faktoren miteinander multiplizierst.
Im Gymnasium und manchmal auch in der Realschule (nur naturwissenschaftlicher Zweig) musst du ab der 9. Klasse auch umgekehrt die allgemeine Form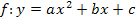 
in die faktorisierte Form umrechnen können.
Die Zerlegung der allgemeinen Form (a,b,c-Form) in die einzelnen Linearfaktoren, nennt man Faktorisieren. Je nach Art des Funktionsterm kann faktorisiert werden, indem man ausklammert, binomische Formeln oder den Satz von Vietaanwendet. (Den Satz von Vieta musst du nicht unbedingt anwenden können. Stattdessen kannst du die im Folgenden beschriebene Methode verwenden;das dauert zwar länger, ist aber sicherer. Den Satz von Vieta wirklich nur verwenden, wenn du ihn gut kannst.)
Falls Ausklammern oder die Anwendung der binomischen Formeln nicht funktionieren, hilft es den zu faktorisierenden Funktionsterm gleich Null zu setzen und z.B. mit der Mitternachtsformel auszurechnen. Das funktioniert zumindest dann immer, wenn sich die Funktion überhaupt faktorisieren lässt, d.h. wenn sie überhaupt Nullstellen hat. Vergleiche dazu die folgenden Beispiele!
1. Bsp.: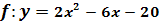 
Die Funktion soll vollständig faktorisiert, also in ihre Linearfaktoren zerlegt werden.
Lösung:
Man könnte zuerst die Zahl 2 ausklammern und danach den Satz von Vietaanwenden.
