Einführung in die quadratischen Funktionen
Nun wirst du dich sicher fragen, wie man den Scheitel ermittelt, wenn b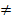 
0 ist. Das ist nicht so einfach. Liegt eine quadratische Funktion in ihrer allgemeinen Form 
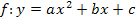vor und b ist nicht gleich Null, kann man den Scheitel nicht direkt ablesen. D.h. wenn neben 
auch x (ohne Quadrat) im Funktionsterm vorkommt, kannst du den Scheitel und somit die Verschiebung der Parabel im Koordinatensystem, nicht direkt von b und c ablesen.
Es gibt aber eine andere Form der quadratischen Funktion, aus der sich der Scheitel sofort ablesen lässt, die sogenannte Scheitelform einer Parabel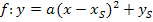 
.
Neben der allgemeinen Form und der Scheitelform 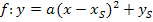existiert eine dritte Form, die faktorisierte Form (Produktform) der Parabel 
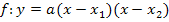, wobei 
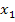und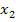 
die x-Koordinaten der Nullstellen der Parabel sind. Hat eine Parabel keine Nullstellen, weil sie die x-Achse gar nicht schneidet, gibt es keine faktorisierte Form dieser Parabel.
Beispiel:Zeige, dass die folgenden Funktionsgleichungen die gleiche Parabel beschreiben!
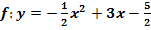(Allgemeine Form der Parabel)
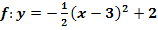(Scheitelform der gleichen Parabel)
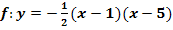(Faktorisierte Form der gleichen Parabel)
Lösung:
Auf den ersten Blick ist eigentlich nicht erkennbar, dass es sich jedes Mal um die gleiche Parabel handelt. Wenn man aber sowohl die Scheitelform als auch die faktorisierte Form jeweils ausrechnet, d.h. die Klammern auflöst und soweit möglich zusammenfasst, kannst man leicht zeigen, dass sich wieder die als erstes gezeigte allgemeine Form von f ergibt.
Umwandlung der Scheitelform in die allgemeine Form:
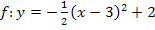2. Binomische Formel 
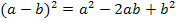anwenden!
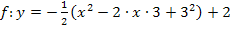
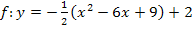
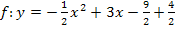
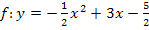
Umwandlung der faktorisierten Form in die allgemeine Form:
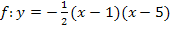
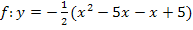
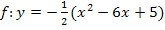
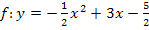
Nun ist gezeigt, dass es sich wirklich um die gleiche Funktion, nur in verschiedenen Formen, handelt.
Wie man an diesem Beispiel erkennen kann, ist es nicht besonders schwer, die Scheitelform bzw. die faktorisierte Form der Parabel in die allgemeine Form umzurechnen. Umgekehrt von der allgemeinen Form in die Scheitelform oder faktorisierte Form umzurechnen, verlangt deutlich mehr rechnerisches Geschick. Wie die Umwandlung in die Scheitelform funktioniert, findest du unter Quadratische Ergänzung (zur Scheitelberechnung). Die Umrechnung in die faktorisierte Form wird bei Faktorisierte Form (Produktform) einer quadratischen Funktion ausführlich erläutert.
