Einführung in die quadratischen Funktionen
Die Funktion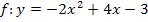 
ist beispielsweise eine nach unten geöffnete, schmälere Parabel. Da a = -2 negativ ist, ist die Parabel nach unten geöffnet. Der Betrag von a ist hier 
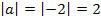, d.h. es gilt: 
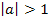Daher ist die Parabel schmäler als die Normalparabel.
TIPP:
Mit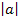 
ist im Prinzip die Zahl vor 
ohne ihrem Vorzeichen gemeint. Der Betrag einer Zahl ist bekanntlich immer positiv, d.h. man soll das Vorzeichen weglassen. Um zu entscheiden, ob eine Parabel breiter oder schmäler ist als die Normalparabel, nimmst du deshalb einfach die Zahl vor 
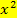, also a, und lässt das Vorzeichen weg. Ist diese Zahl kleiner als Eins, ist die Parabel breiter als die Normalparabel. Ist diese Zahl größer als Eins, ist die Parabel schmäler als die Normalparabel. Das Vorzeichen von a gibt nur an, ob die Parabel nach oben (a ist positiv) oder nach unten (a ist negativ) geöffnet ist, es hat jedoch nichts mit der Öffnungsweite der Parabel zu tun.
Nun möchtest du bestimmt wissen, was b und c mit der Lage der Parabel im Koordinatensystem zu tun haben. Das lässt sich leider nicht so einfach sagen. b hat zwar etwas mit der Seitwärtsverschiebung zu tun und c hat etwas mit der Verschiebung nach oben bzw. unten zu tun. Doch leider kann man nur für b = 0, d.h. wenn x ohne Quadrat in der Funktionsgleichung fehlt, sagen, dass die Parabel um c nach oben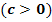 
bzw. um c nach unten 
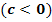verschoben ist. Für 
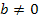gibt es keinen sofort erkennbaren Zusammenhang zwischen b, c und der Verschiebung der Parabel.
Will man den Graph einer Parabel zeichnen, ist es hilfreich ihren Scheitelpunkt zu kennen. Oft wird in Aufgaben auch speziell nach den Koordinaten des Scheitels gefragt. Aus der allgemeinen Form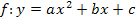 
lässt sich der Scheitel allerdings nur für b = 0 direkt ablesen. Ist b gleich Null, fällt das x (ohne Quadrat) weg, wegen 
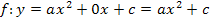. Nur wenn das x (ohne Quadrat) fehlt, kann man den Scheitel in der allgemeinen Form (a,b,c-Form) sofort erkennen. Eine Parabel der Form 
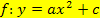ist um c nach oben bzw. nach unten verschoben, nicht aber nach links oder rechts. Der Scheitel liegt daher für b = 0 auf der y-Achse bei 
.
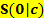Beispiele:
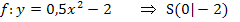Die Parabel ist also um 2 nach unten verschoben.
Wegen a = 0,5 ist die Parabel außerdem breiter als die Normalparabel, da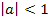 
. Weil 
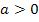ist, ist die Parabel nach oben geöffnet.
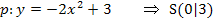
Die Parabel ist also um 3 nach oben verschoben.
Wegen a = -2 ist die Parabel außerdem schmäler als die Normalparabel, da 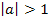. Weil 
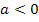ist, ist sie nach unten geöffnet.
