Einführung in die quadratischen Funktionen
Beispielsweise stellt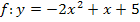 
eine nach unten geöffnete Parabel dar, weil a = -2 negativ ist.
Ist a = 1 oder a = -1, liegt eine Normalparabel vor. Immer wenn keine Zahl vor dem 
steht, hast du also die Gleichung einer Normalparabel vor dir. Du kannst dann die Schablone für Parabeln zum Zeichnen verwenden. Für a = 1 erhält man eine nach oben geöffnete Normalparabel, für a = -1 eine nach unten geöffnete Normalparabel.
Beispielsweise stellt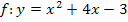 
eine nach oben geöffnete Normalparabel dar, weil man die Funktion auch ausführlich schreiben kann als 
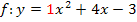, und daher a = 1 ist. Umgekehrt ist der Graph der Funktion 
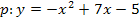eine nach unten geöffnete Parabel, denn 
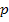lässt sich schließlich auch in der Form 
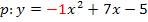schreiben. Weil a = -1 ist, muss eine nach unten geöffnete Normalparabel vorliegen.
Wenn a = 1 ist, wird aus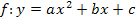 
natürlich immer 
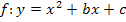. Diese Form einer quadratischen Funktion wird als normierte Form oder Normalform einer Parabel bezeichnet. Die normierte Form/ Normalform 
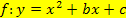beschreibt wegen a = 1 ausschließlich nach oben geöffnete Normalparabeln. Statt den Buchstaben b und c werden in der Normalform, also wenn a = 1 ist, manchmal auch p an Stelle von b und q anstatt c verwendet. Daher findet sich in manchen Lehrbüchern und Formelsammlungen auch die Schreibweise 
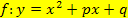als Gleichung einer nach oben geöffneten Normalparabel. Wir bleiben auf dieser website jedoch bei den Bezeichnungen a, b, c für die Koeffizienten bei quadratischen Funktionen.
Parabeln, die breiter oder schmäler sind als die Normalparabel:
Breitere Parabeln (d.h. gestaucht entlang der y-Achse):
Für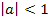 
ist eine Parabel breiter als die Normalparabel. 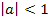kann auch in der Form 
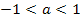geschrieben werden und bedeutet nichts anderes, als dass a zwischen -1 und +1 liegen soll;a muss also ein echter Bruch sein, damit die Parabel breiter ist als die Normalparabel. Je kleiner der Betrag von a ist, desto breiter ist die Parabel.
Beispielsweise ist die Parabel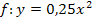 
noch breiter als die Parabel 
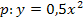. Aber auch 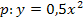ist schon breiter als die Normalparabel, da a = 0,5 kleiner ist als die Zahl 1. Beide Parabeln sind nach oben geöffnet, da a bei beiden Parabeln positiv ist.
Schmälere Parabeln (d.h. gestreckt entlang der y-Achse):
Für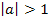 
ist eine Parabel schmäler als die Normalparabel. 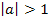bedeutet nichts anderes, als dass 
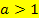oder 
sein muss. Ist a größer als 1 oder kleiner als -1, dann ist die Parabel schmäler als eine Normalparabel. Je größer der Betrag von a ist, desto schmäler ist die Parabel. Warum das so ist, wird weiter unten noch ausführlich erklärt.
