Einführung in die quadratischen Funktionen
Die bei der letzten Funktion ursprünglich gegebene Form, also die mit den beiden Klammern, wird als Faktorisierter Funktionsterm oder als faktorisierte Form der Funktionsgleichung bezeichnet. Es handelt sich daher bei der faktorisierten Form um die Produktform der Funktion. Wie man von der allgemeinen Form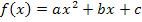 
auf die faktorisierte Form kommt, wird im Kapitel Faktorisierte Form (Produktform) einer quadratischen Funktion gezeigt.
Gegenbeispiele: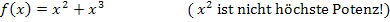 
Der Graph einer quadratischen Funktion ist immer eine sogenannte Parabel. Siehe Abbildung!
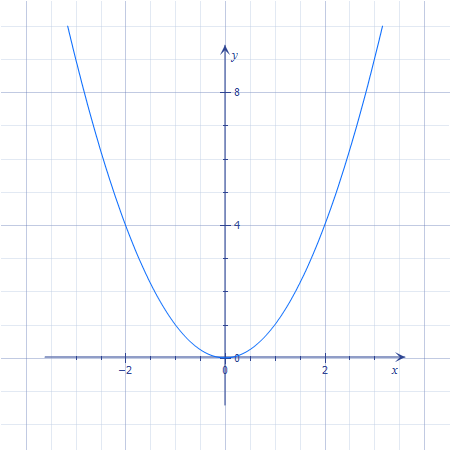
Abb. Der Graph der Normalparabel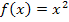 
Warum der Graph einer quadratischen Funktion eine solche Form hat, wird klar, sobald man sich die einfachste quadratische Funktion 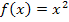genauer ansieht. Da 
eine gerade Potenz ist, ergeben sich immer positive Werte für den Funktionswert, egal ob man positive oder negative Zahlen einsetzt. (Ausnahme:Für x = 0 ergibt sich 
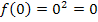) Wir setzen nun beispielsweise 
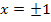und vergleichen die Funktionswerte:
= 
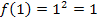
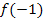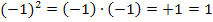
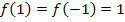
Es ergeben sich, wie auf Grund der geraden Potenz erwartet, die gleichen Funktionswerte. Das kannst du nun auch mit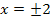 
oder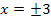 
nachrechnen.
= 
= 
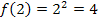
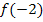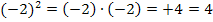
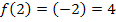
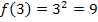
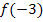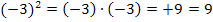
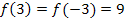
Allgemein kann man schreiben: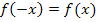 
Das bedeutet, dass die Funktion achsensymmetrisch zur y-Achse ist. (Mehr zum Symmetrieverhalten von Funktionen im Kapitel Symmetriezum Koordinatensystem)
Außerdem kann man feststellen, dass für positive x die Funktionswerte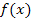 
immer schneller zunehmen, je größer der Betrag des eingesetzten x-Wertes ist. In einfacheren Worten:Je größer x (ohne Vorzeichen) ist, desto stärker nimmt der y-Wert der Funktion zu. Es kann sich daher nicht um ein lineares Wachstum handeln, denn dabei nimmt der Funktionswert 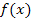bzw. y gleichmäßig zu. Damit du selbst die Funktion 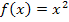leicht zeichnen kannst, sind hier noch einmal alle bereits berechneten Funktionswerte in einer Wertetabelle zusammengestellt:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
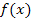9 | 4 | 1 | 0 | 1 | 4 | 9 |
Diese Punkte kannst du nun in ein Koordinatensystem einzeichnen und weich miteinander verbinden. So erhältst du die oben dargestellte Parabel.
Für die in der Abbildung gezeigte Parabel gibt es sogar Schablonen, die das Zeichnen erleichtern. (Achtung:Die Schablone kann nur verwendet werden, wenn auf beiden Achsen des Koordinatensystems der Maßstab 1 LE =1cm, also normaler cm-Maßstab, gilt.) Man muss sich aber nicht unbedingt so eine Schablone kaufen. Man kann eine Parabel natürlich auch mit einer Wertetabelle frei Hand zeichnen.
