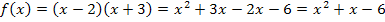Einführung in die quadratischen Funktionen
Wie der Name schon verrät, ist eine quadratische Funktion eine Funktion, die 
enthält. Genauer gesagt:Unter einer quadratischen Funktion versteht man eine Funktion vom folgenden Typ:
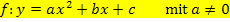
Diese Form nennt man „allgemeine Form“ einer quadratischen Funktion.
Andere gleichbedeutende, oft verwendete Schreibweisen sind:
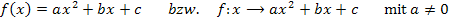
Da der Koeffizient a (= Zahl vor ) nicht gleich Null sein darf, handelt es sich bei einer quadratischen Funktion immer um eine Funktion, deren Funktionsgleichung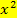 
als höchste Potenz enthält. ( darf dabei nicht im Nenner eines Bruchs stehen, denn sonst läge eine gebrochenrationale Funktion vor. Der Graph, d.h. die Kurve im Koordinatensystem, einer Funktion mit x im Nenner sieht ganz anders aus als der einer quadratischen Funktion! Kommt bei einer Funktion x im Nenner vor, kann es keine quadratische Funktion sein, auch wenn vorkommt.) Ob neben auch zusätzlich x (genauer gesagt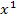 
) oder eine Konstante c, d.h. Zahl ohne x, im Funktionsterm vorkommt, ist egal. Hauptsache die Funktionsgleichung enthält ein 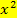, keine höhere Potenz von x und kein x im Nenner. Dann liegt eine quadratische Funktion vor.
Beispiele: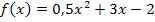 
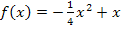
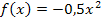
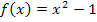
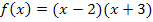
Beim letzten Beispiel ist es nicht direkt erkennbar, dass eine quadratische Funktion vorliegt. Multipliziert man jedoch die Klammern aus, wird klar, dass es sich auch bei dieser Funktion um eine quadratische Funktion handelt.
