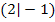Scheitelberechnung mit Hilfe der Nullstellen
Sind die Nullstellen einer Parabel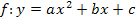 
oder 
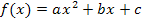bereits bekannt, lässt sich die x-Koordinate des Scheitels ganz leicht berechnen. Auf Grund der Symmetrie der Parabel muss die x-Koordinate des Scheitels 
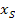genau in der Mitte zwischen den beiden Nullstellen der Parabel liegen.
Besonders leicht lassen sich die Nullstellen einer Parabel an der faktorisierten Form /Produktform der Parabel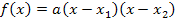 
ablesen. Siehe dazu auch:Faktorisierte Form (Produktform) einer quadratischen Funktion
Dabei sind 
und 
die x-Koordinaten der Nullstellen. Für die x-Koordinate des Scheitels gilt dann:
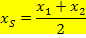
Die y-Koordinate des Scheitels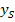 
berechnet man, indem man den soeben berechneten Wert 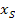in die Funktionsgleichung der Parabel für x einsetzt.
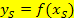
Beispiel:
Gegeben ist die Funktion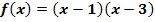 
. Es soll der Scheitel dieser Funktion bestimmt werden.
Lösung:
Da die Funktion in ihrer faktorisierten Form (Produktform) vorliegt, lassen sich ihre Nullstellen ganz leicht ablesen.
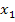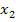Um den Scheitel zu berechnen, ermitteln wir daher zuerst die Nullstellen und von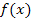 
und bilden danach den Mittelwert (Durchschnittswert) von 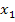und 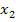. So erhalten wir die x-Koordinate des Scheitels .
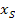Nullstellen: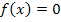 
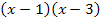= 0
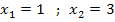
Anmerkung:Da ein Produkt gleich Null ist, wenn einer der Faktoren gleich Null ist, dürfen die beiden Klammern einzeln gleich Null gesetzt werden. Die erste Klammer wird Null, wenn man für x die Zahl 1 einsetzt. Die zweite Klammer wird Null, wenn man für x die Zahl 3 einsetzt. So erhält man ganz schnell die beiden Lösungen der Gleichung.
Natürlich hätte man die beiden Klammern auch ausmultiplizieren können. Dann hätte man die gemischtquadratische Gleichung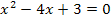 
erhalten, die man jedoch nur viel umständlicher nach x hätte auflösen können, beispielsweise mit der sogenannten Mitternachtsfomel. Daher solltest du die Klammern hier besser nicht ausmultiplizieren!
Berechnung des Scheitels:
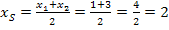
Die y-Koordinate des Scheitels 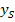erhalten wir durch einsetzen von 
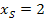in die Funktionsgleichung.
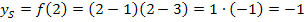
Scheitel S 
