Scheitelberechnung mit Hilfe der Differenzialrechnung
Der Scheitelpunkt einer Parabel ist nichts anderes als das Extremum der quadratischen Funktion 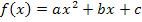 mit
mit 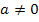 . Da bei einem Extremum die Tangente an den Graph der Funktion
. Da bei einem Extremum die Tangente an den Graph der Funktion 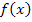 waagrecht verläuft, muss die Steigung, d.h. die erste Ableitung
waagrecht verläuft, muss die Steigung, d.h. die erste Ableitung 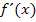 , gleich Null sein. Man muss daher nur die erste Ableitung bilden und gleich Null setzen, um die x-Koordinate des Scheitels
, gleich Null sein. Man muss daher nur die erste Ableitung bilden und gleich Null setzen, um die x-Koordinate des Scheitels 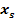 zu berechnen. Die y-Koordinate des Scheitels
zu berechnen. Die y-Koordinate des Scheitels 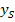 erhält man, wenn man
erhält man, wenn man 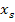 in die Funktionsgleichung
in die Funktionsgleichung 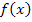 einsetzt. (Wie du weißt, ist
einsetzt. (Wie du weißt, ist 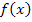 nur eine andere Schreibweise für y.)
nur eine andere Schreibweise für y.)
Scheitel = Extremum![]() ⇔
⇔ 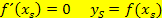
Vorsicht:Du darfst x nicht etwa in die Ableitung 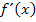 einsetzen, wenn du die zugehörige y-Koordinate berechnen willst. Durch das Einsetzen von x in die erste Ableitung ergibt sich nämlich nicht der y-Wert, sondern die Steigung der Funktion an dieser Stelle. Würdest du
einsetzen, wenn du die zugehörige y-Koordinate berechnen willst. Durch das Einsetzen von x in die erste Ableitung ergibt sich nämlich nicht der y-Wert, sondern die Steigung der Funktion an dieser Stelle. Würdest du 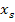 in
in 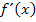 einsetzen, würde sich wieder Null ergeben, da am Scheitel die Steigung von
einsetzen, würde sich wieder Null ergeben, da am Scheitel die Steigung von 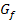 gleich Null ist. Durch
gleich Null ist. Durch 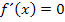 haben wir
haben wir 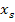 schließlich ermittelt!
schließlich ermittelt!
Bsp.:
Berechne mit Hilfe der Differenzialrechnung die Koordinaten des Scheitelpunkts S der Parabel 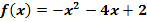 !
!
Lösung:
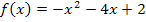
Scheitel (Extremum): 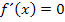
Wir bilden zuerst die erste Ableitung 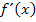 .
.
Erinnere dich an die Ableitungsregel:![]()
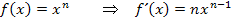
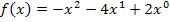
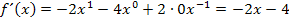
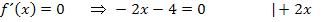
![]()

![]()
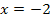
Nun haben wir die x-Koordinate des Scheitels ermittelt und es fehlt nur noch die y-Koordinate des Scheitels. Dazu setzen wir x = -2 in 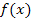 ein;wir bilden also
ein;wir bilden also 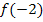 .
.
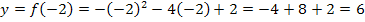
Der Scheitel hat daher die Koordinaten S(-2| 6).
Die Verwendung der Differenzialrechnung, d.h. der Ableitung 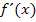 der Funktion
der Funktion 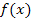 , ermöglicht es uns, den Scheitel einer Parabel sehr schnell und bequem zu berechnen. Die Methode der quadratischen Ergänzung, die du in der Mittelstufe zur Scheitelberechnung verwenden musstest, und die dir wahrscheinlich nur noch in vager Erinnerung ist, kannst du dank der Differenzialrechnung getrost vergessen. Durch die Verwendung der Ableitung lassen sich auch die Extrema von Polynomfunktionen dritten und höheren Grades, sowie anderer Funktionen berechnen. Mehr dazu im Kapitel:Einführung in die Differenzialrechnung
, ermöglicht es uns, den Scheitel einer Parabel sehr schnell und bequem zu berechnen. Die Methode der quadratischen Ergänzung, die du in der Mittelstufe zur Scheitelberechnung verwenden musstest, und die dir wahrscheinlich nur noch in vager Erinnerung ist, kannst du dank der Differenzialrechnung getrost vergessen. Durch die Verwendung der Ableitung lassen sich auch die Extrema von Polynomfunktionen dritten und höheren Grades, sowie anderer Funktionen berechnen. Mehr dazu im Kapitel:Einführung in die Differenzialrechnung

