Quadratische Ergänzung (zur Scheitelberechnung)
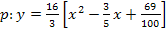
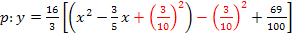
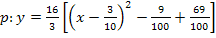
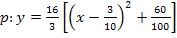
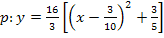
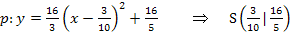
Hier das Ergebnis noch einmal, aber mit Dezimalzahlen geschrieben, soweit das ohne Runden möglich ist:
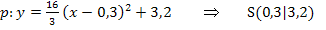
Und zum Abschluss noch ein Anwendungsbeispiel:
2. Bsp.:
Peter ist ein 1,80 Meter großer Junge. Wir denken uns seinen Körperschwerpunkt in Höhe seines Bauchnabels, welcher sich 112,5 cm über dem Boden befindet. Nun springt Peter von einem 5-Meter-Brett ins Wasser. Sein Körperschwerpunkt beschreibt dabei eine parabelförmige Flugbahn mit der Gleichung 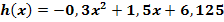 , wobei x die Sprungweite in Meter und
, wobei x die Sprungweite in Meter und 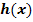 die Höhe des Körperschwerpunkts über der Wasseroberfläche auch in Metern darstellt.
die Höhe des Körperschwerpunkts über der Wasseroberfläche auch in Metern darstellt.
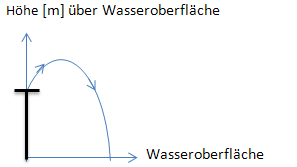
Welche maximale Höhe über der Wasseroberfläche erreicht Peter (genau genommen sein Körperschwerpunkt)?
Lösung:
Es handelt sich bei der Funktion 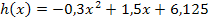 um eine quadratische Funktion. Daher ist der Graph natürlich eine Parabel. Die Parabel ist nach unten geöffnet, da
um eine quadratische Funktion. Daher ist der Graph natürlich eine Parabel. Die Parabel ist nach unten geöffnet, da 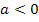 ist.
ist.
(Wiederholung:a ist die Zahl, welche vor  steht. Wenn a negativ ist, ist die Parabel nach unten geöffnet!).
steht. Wenn a negativ ist, ist die Parabel nach unten geöffnet!).
Weil die Parabel nach unten geöffnet ist, ist der Scheitel das absolute Maximum. Wir müssen daher den Scheitelpunkt der Funktion h berechnen. Dazu benötigt man die Scheitelform der Parabel. Man erhält sie, indem man zuerst a ausklammert und danach quadratisch ergänzt:
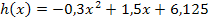
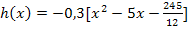
![]() 1. Schritt: a ausklammern
1. Schritt: a ausklammern
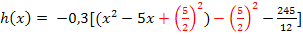 2. Schritt: Quadratische Ergänzung
2. Schritt: Quadratische Ergänzung
![]() (d.h. wir ergänzen zu einer binomischen
(d.h. wir ergänzen zu einer binomischen
![]() Formel, indem wir die Zahl vor dem x
Formel, indem wir die Zahl vor dem x
![]() halbiert und danach quadriert zuerst
halbiert und danach quadriert zuerst![]() addieren und dann wieder subtrahieren)
addieren und dann wieder subtrahieren)
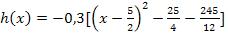
![]() 3. Schritt:Binomische Formel umformen
3. Schritt:Binomische Formel umformen
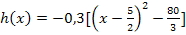
![]() Zusammenfassen
Zusammenfassen
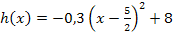
![]() 4. Schritt:a in die eckige Klammer hineinmultiplizieren
4. Schritt:a in die eckige Klammer hineinmultiplizieren![]()
Umgerechnet in Dezimalzahlen:![]() Vergleiche:Scheitelform (allgemein):
Vergleiche:Scheitelform (allgemein):
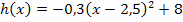
![]()
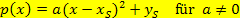
 Scheitel S (2,5| 8 )
Scheitel S (2,5| 8 )![]() Scheitel S(
Scheitel S( 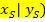
Die y-Koordinate des Scheitels ist 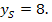
D.h. Peter erreicht eine maximale Sprunghöhe von 8m.
- Page 4 of 4
- « Previous
- 1
- 2
- 3
- 4
- Next »

