Quadratische Ergänzung (zur Scheitelberechnung)
Scheitelkoordinaten ablesen:
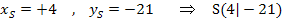
Teilaufgabe c)
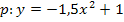
Jetzt wirst du dich sicher fragen, wie du bei dieser Aufgabe quadratisch ergänzen sollst, wenn doch gar kein x (ohne Quadrat) im Funktionsterm vorkommt. Die Antwort auf diese Frage ist ganz einfach:Gar nicht! Du kannst und brauchst hier überhaupt nicht quadratisch ergänzen! Der Scheitel lässt sich nämlich direkt ablesen, weil die Parabel nur auf der y-Achse um 1 nach oben verschoben ist, aber nicht zur Seite. Der Scheitel hat deshalb die x-Koordinate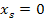 
und die y-Koordinate 
.
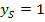S(0| 1)
Merke:Jede Parabel der Form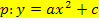 
hat den Scheitel S(0| c).
Also niemals versuchen quadratisch zu ergänzen, wenn nur 
aber kein x (ohne Quadrat) im Funktionsterm vorkommt!
Teilaufgabe d)
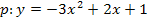
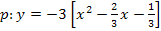
Vorsicht beim Ausklammern einer negativen Zahl! Dabei drehen sich alle Vorzeichen um!
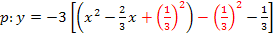Zur Erinnerung:Ein Bruch wird halbiert, indem man entweder den Zähler halbiert (wenn sich keine Kommazahl ergibt) oder den Nenner verdoppelt.
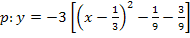
Ein Bruch wird quadriert, indem Zähler und Nenner einzeln quadriert werden. Der hinterste Bruch wird bereits auf den gleichen Nenner
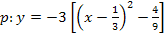
gebracht, damit im nächsten Schritt leichter zusammengefasst werden kann. (Du kannst die letzten beiden Brüche natürlich auch einfach mit dem Taschenrechner zusammenfassen.)
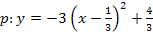
-3 wieder in die eckige Klammer hineinmultiplizieren, aber nicht in die Runde! Also -3 vor die runde Klammer schreiben und mit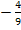 
multiplizieren. Dabei das Kürzen nicht vergessen!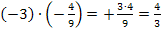 
Scheitelkoordinaten ablesen:
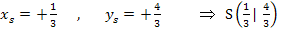
Teilaufgabe e)
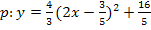
Dieser Funktionsterm liegt noch nicht in der Scheitelform vor, auch wenn es fast danach aussieht. Das Problem ist die 2 vor dem x in der Klammer.
Erinnere dich an die Scheitelform einer Parabel: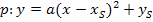 
Vor dem x in der Klammer der Scheitelform steht kein Koeffizient, also keine Zahl! In der angegebenen Funktionsgleichung, steht dagegen die Zahl 2 vor dem x in der Klammer. Der Scheitel kann daher nicht direkt abgelesen werden.
Um den Scheitel der gegebenen Parabel zu ermitteln, muss zuerst mit Hilfe der zweiten binomischen Formel die Klammer quadriert, danach der Faktor 
in die Klammer hinein multipliziert und soweit möglich zusammengefasst werden. Danach liegt die Parabel in ihrer allgemeinen Form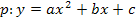 
vor und kann mittels quadratischer Ergänzung in ihre Scheitelform umgewandelt werden. Daraus lässt sich dann letztendlich der Scheitel ablesen.
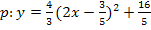
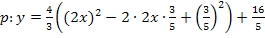
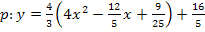
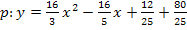
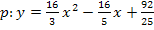(Allgemeine Form der Parabel)
Nun wandeln wir die allgemeine Form der Parabel in die Scheitelform um.
