Quadratische Ergänzung (zur Scheitelberechnung)
Falls dein Lehrer in der Schule a nicht komplett ausklammert, sondern nur aus den ersten beiden Faktoren und nicht aus der letzten Zahl, wundere dich bitte nicht. Auch das ist richtig. Es gibt hier leider ´mal wieder zwei verschiedene Rechenwege. Vor allem manche Realschullehrer wählen diese Methode. Schau bitte in deinem Schulheft nach, wie dein(e) Lehrer(in) das macht. Hat er/sie a nur aus den ersten beiden Faktoren, also aus 
und x ausgeklammert, jedoch nicht aus der Zahl ohne x, verfährst du ebenfalls nach diesem Rechenweg. Du findest eine ausführliche Anleitung zu diesem Weg bei Scheitelberechnung durch quadratische Ergänzung (Variante:a nicht komplett ausklammern)
Da die quadratische Ergänzung den meisten Schülern anfangs Probleme macht, werden im Folgenden noch weitere Aufgabenbeispiele, vollständig durchgerechnet, gezeigt.
1. Bsp.:
Berechne, wenn nötig mittels quadratischer Ergänzung, den Scheitel der folgenden Parabeln!
a)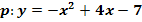 
b)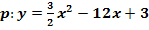 
c)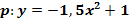 
d)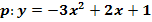 
e)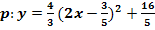 
Lösung:
Damit du die einzelnen Rechenschritte besser nachvollziehen kannst, findest du zu jedem einzelnen Schritt rechts daneben eine Erklärung.
Teilaufgabe a)
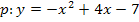
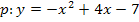
a = -1 (d.h. das Minus-Zeichnen) ausklammern 
Vorzeichen umdrehen
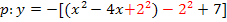
Quadratische Ergänzung:Zahl vor dem x halbieren und quadrieren, zuerst + dann gleich wieder – rechnen
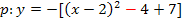
2. Binomische Formel anwenden und beginnen den hinteren Teil auszurechnen. Vorsicht:Das Quadrat bei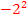 
bezieht sich nur auf die 2, nicht aber auf das Minus-Zeichen. So ergibt sich: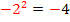 
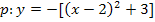
Zusammenfassen
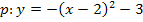
Eckige Klammer auflösen
Scheitelkoordinaten ablesen:
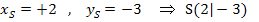
Beachte, dass du das Vorzeichen bei der Zahl in der Klammer umdrehen musst, um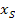 
zu ermitteln. (Zur Kontrolle kannst du die x-Koordinate des Scheitels für x in die Klammer einsetzen;dann muss sich Null ergeben.) Um 
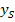zu erhalten, nimmt man einfach die Zahl hinter der Klammer, allerdings ohne das Vorzeichen umzudrehen!
Zahl in der Klammer mit umgedrehtem Vorzeichen 
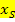
Zahl hinter der Klammer (Vorzeichen lassen, wie es ist) 
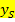
Teilaufgabe b)
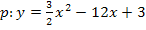
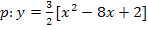a =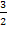 
ausklammern, d.h. jeden Faktor durch 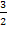teilen bzw. mit dem Kehrwert 
multiplizieren (Zur Not mit dem Taschenrechner!)
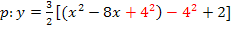
Quadratische Ergänzung:Zahl vor dem x halbieren und quadrieren, zuerst + dann gleich wieder – rechnen
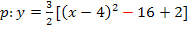
2. Binomische Formel anwenden
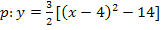
Zusammenfassen
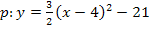
Eckige Klammer auflösen, d.h. 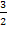vor die runde Klammer schreiben und mit der Zahl -14 multiplizieren
