Formel zur Scheitelberechnung
Mit Hilfe der quadratischen Ergänzung kann die folgende Formel zur Berechnung der Scheitelkoordinaten einer Parabel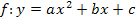 
hergeleitet werden.
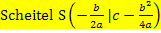oder: Scheitel S( 
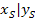) mit 
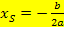und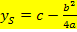 
Mit dieser Formel ist es ganz leicht den Scheitel einer Parabel zu berechnen. Du kannst diese Formel entweder auswendig lernen oder einfach in der Formelsammlung nachschauen. In der Formelsammlung für Realschulen findest du sie bei den quadratischen Funktionen.
Du musst diese Formel nicht selbst herleiten können. Wenn es dich aber doch interessiert, woher sie kommt, gehe zu: Herleitung der Formel zur Scheitelberechnung
Vorsicht:Achte beim Einsetzen in die oben gezeigte Formel für die Scheitelkoordinaten besonders auf die Vorzeichen! Erfahrungsgemäßkommt es hierbei immer wieder zu Fehlern.
Bsp.:
Berechne mit Hilfe der Formel für die Scheitelkoordinaten den Scheitel S der Parabel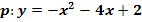 
!
Lösung:
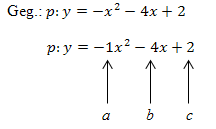
Wir lesen zuerst die Koeffizienten a, b und c aus der Funktionsgleichung ab.
a = -1 ;b = – 4 ; c = 2
Nun können diese Werte in die Formel für die Scheitelkoordinaten eingesetzt werden.
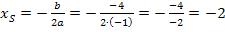
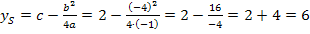
Der Scheitel hat die Koordinaten S(-2| 6).
Die Formel zur Berechnung der Scheitelkoordinaten kann auch zur Extremwertberechnung von quadratischen Termen verwendet werden, da es sich beim Scheitel schließlich um den höchsten bzw. tiefsten Punkt der Parabel, den sogenannten Extrempunkt, handelt. In den Abschlussprüfungen an nicht-naturwissenschaftlichen Realschulen werden solche Aufgaben sehr oft gestellt. Durch die Verwendung der Formel ersparst du dir die aufwendige Rechnung der quadratischen Ergänzung. Die Formel ist aber meist erst ab der 10. Klasse erlaubt. Frage sicherheitshalber deinen Lehrer in der Schule, ob du statt der quadratischen Ergänzung auch die Formel für die Scheitelberechnung verwenden darfst.
Für Schüler der Realschule:Mehr zum Thema „Extremwertaufgaben“ gibt es im Kapitel:Funktionale Abhängigkeiten
Für Schüler eines Gymnasiums ab der 11. Klasse oder einer FOS/BOS:Anspruchsvollere Aufgabenbeispiele rund um das Thema „Extremwertaufgaben“ findest du im Kapitel: Extremwertaufgaben/Optimierungsprobleme
