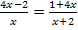Rechnerische Lösungsverfahren von Bruchgleichungen
Welches Verfahren, wann anwenden?
Bei welchen Bruchgleichungen du das zweite Verfahren direkt anwenden kannst, ist leicht zu erklären:
Wenn auf beiden Seiten der Gleichung jeweils ein einzelner Bruch steht, multiplizierst du grundsätzlich kreuzweise.
Aber was soll man nun bei Bruchgleichungen machen, die nicht in der der Form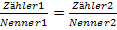 
vorliegen. Diese Frage lässt sich nicht allgemein beantworten. Du kannst sowohl das 1. Verfahren als auch das 3. Verfahren anwenden oder erst einmal die Gleichung auf die Form 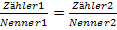bringen und dann kreuzweise multiplizieren, also letztendlich das 2.Verfahren anwenden. Insofern sind alle drei Rechenwege anwendbar. Du solltest die verschiedenen Methoden einfach ´mal selbst ausprobieren, um herauszufinden, was dir persönlich am leichtesten fällt. Außerdem wäre es hilfreich, wenn du in dein Mathe-Schulheft schaust, um festzustellen, wie es dein Lehrer in der Schule macht. Die meisten Lehrer wollen, dass du den Rechenweg verwendest, den sie selbst im Unterricht gezeigt haben.
So, nun kommen wirklich keine weiteren Verfahren mehr dazu! Jetzt geht es also nur noch an´s Üben. Weil das mit den Bruchgleichungen anfangs für die meisten Schüler nicht so einfach ist, sollen die eben vorgestellten rechnerischen Lösungsverfahren von Bruchgleichungen an vielen weiteren Aufgaben erläutert werden. Also keine Sorge, wenn dir das im Moment alles noch nicht so wirklich klar ist. Es kommen noch ganz viele Beispiele und daran kannst du sehen, wie es funktioniert. Auch wie man den Hauptnenner in schwierigeren Fällen überhaupt findet, wird noch ausführlich erklärt. Außerdem folgen noch einige wichtige Tipps. Also, weiter mit der nächsten Teilaufgabe!
zu 1d.)
Hier noch einmal die Angabe:
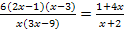
Lösung:
Wie immer geht es los mit der Definitionsmenge. Wir klammern bei der Klammer im Nenner des linken Bruchs erst einmal die Zahl 3 aus. Danach lässt sich die Definitionsmenge viel besser erkennen.
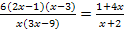
Jetzt kann man die Definitionsmenge leicht ablesen: D = ℚ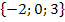 
Wenn du nicht verstehst, wie man auf die Definitionsmenge kommt, lies bitte die Erklärungen im Kapitel Definitionsmenge einer Bruchgleichung!
Jetzt wollen wir uns daran machen die Gleichung zu lösen:
Als erstes kürzen wir den Faktor (x – 3). Damit wird die ganze Sache schon etwas einfacher.
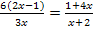
Die 3 lässt sich natürlich auch noch kürzen:
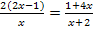
Im Zähler des ersten Bruchs multiplizieren wir noch die 2 in die Klammer hinein.
