Rechnerische Lösungsverfahren von Bruchgleichungen
Jetzt multiplizieren wir mit dem Hauptnenner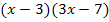 
. Er lässt sich komplett wegkürzen, so dass der Nenner auf beiden Seiten der Gleichung wegfällt.
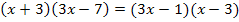
An Stelle des Multiplizierens mit dem Hauptnenner und nachfolgendem Kürzen kann man, wie du siehst, auch einfach nur die Zähler gleichsetzen. Der Hauptnenner wird dabei also einfach weggelassen. Das sieht dann ohne die ganzen Zwischenschritte folgendermaßen aus:
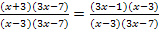
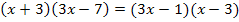
Dies ist natürlich genau die selbe Gleichung, die wir schon bei den anderen beiden Verfahren erhalten haben. Daher wollen wir hier die Gleichung nicht noch einmal lösen;das haben wir ja schon beim ersten Verfahren gemacht. Es sollte hiermit vor allem gezeigt werden, dass man auch nach diesem dritten Verfahren zu der selben Gleichung gelangt.
Das dritte Verfahren zur rechnerischen Lösung von Bruchgleichungen noch einmal in Stichpunkten zusammengefasst:
Vorher Definitionsmenge angeben und nachher Probe machen! |
Jetzt wird dir vermutlich der Kopf nur so schwirren mit all diesen unterschiedlichen Rechenwegen. Um hier wieder Klarheit zu schaffen, noch einmal alle Verfahren kurz zusammengefasst.
Übersicht über die rechnerischen Lösungsverfahren von Bruchgleichungen:
Es gibt drei verschiedene Methoden, wie man Bruchgleichungen nach x auflösen kann. Vorher muss aber immer erst die Definitionsmenge ermittelt und nach der Rechnung sollte die Probe gemacht werden.
1. Direkt mit dem Hauptnenner der gesamten Gleichung multiplizieren
(Vergleiche dazu:Allgemeine Anleitung zur rechnerischen Lösung von Bruchgleichungen) Das funktioniert an sich bei jeder Bruchgleichung.
Bei Gleichungen der Form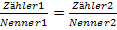 
ist es aber zu umständlich.
2. Kreuzweise Multiplizieren
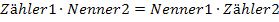
Darf nur verwendet werden, wenn auf beiden Seiten der Gleichung ein einzelner Bruch steht! Ist das noch nicht der Fall kann die Gleichung aber vorher entsprechend umgeformt werden, so dass man danach doch kreuzweise multiplizieren darf.
3. Alles auf den Hauptnenner der gesamten Gleichung bringen und dann nur noch die Zähler der linken und rechten Seite jeweils gleichsetzen.
(Das Weglassen des Hauptnenners entspricht hierbei dem Multiplizieren mit dem Hauptnenner und Kürzen.)
Das funktioniert an sich, wie auch das 1. Verfahren, bei jeder Bruchgleichung. Eigentlich ist diese Methode nur eine Abwandlung des 1. Verfahrens.
Bei Gleichungen der Form 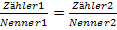ist es aber zu umständlich.
