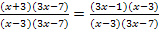Rechnerische Lösungsverfahren von Bruchgleichungen
Da sich jede Bruchgleichung durch geeignetes Erweitern auf die Form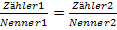 
bringen lässt, kann man letztendlich auch jede Bruchgleichung durch kreuzweises Multiplizieren lösen. Du machst es einfach so, wie es dir lieber ist.
Für Schüler, die sich dafür interessieren, warum das kreuzweise Multiplizieren tatsächlich bei allen Gleichungen der Form 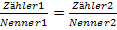dem Multiplizieren mit dem Hauptnenner entspricht, folgt nun eine allgemeine Erklärung:
Wir gehen von einer Bruchgleichung der Form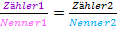 
aus;es steht also auf beiden Seiten der Gleichung jeweils ein einzelner Bruch. Der Hauptnenner sei: 
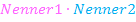Damit multiplizieren wir auf beiden Seiten der Gleichung und kürzen dann soweit möglich. Das Multiplizieren mit dem Hauptnenner ist schließlich die allgemeine Vorgehensweise bei Bruchgleichungen. Danach kürzen wir soweit möglich.
| 
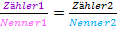
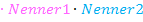
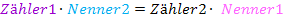
Das entspricht genau dem kreuzweise Multiplizieren.
Wenn du nun denkst, dass das jetzt schon alles zu den rechnerischen Lösungsverfahren von Bruchgleichungen war, muss ich dich leider enttäuschen. Es gibt nämlich noch ein weiteres rechnerisches Lösungsverfahren! Manche Lehrer wenden vor allem bei Bruchgleichungen, die noch nicht die Form 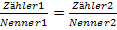haben, ein drittes Verfahren an:
Sie bringen erst einmal alles auf den Hauptnenner (der gesamten Gleichung). Dann multiplizieren sie mit dem Hauptnenner, was dem Weglassen des Nenners auf beiden Seiten entspricht, und lösen die so entstandene Gleichung nach x auf.
Wir werden bei den Teilaufgaben 1e.) und 1f.) noch einmal auf dieses Verfahren zurückkommen, weil es bei diesen Bruchgleichungen wirklich gut funktioniert. Für die vorliegende Gleichung ist es jedoch weniger zu empfehlen, denn hier kann man ja direkt kreuzweise multiplizieren und das ist viel einfacher.
Um zu zeigen, wie dieses dritte Verfahren konkret funktioniert, wenden wir es dennoch auf diese Teilaufgabe an, obwohl es nicht der geschickteste Weg ist.
Hier noch einmal die Gleichung: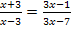 
D = ℚ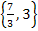 
Der Hauptnenner der gesamten Gleichung ist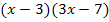 
. Wir erweitern alle beteiligten Terme so, dass sie nachher alle den Nenner 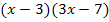besitzen. Den Bruch auf der linken Seite erweitern wir daher mit 
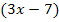und den Bruch auf der rechten Seite mit 
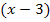. So erhalten wir:
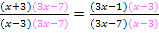
Wir können beim rechten Bruch die Faktoren im Nenner natürlich auch von der Reihenfolge her vertauschen. Es sieht einfach übersichtlicher aus, wenn der Nenner auf beiden Seiten in der gleichen Reihenfolge geschrieben wird.
