Rechnerische Lösungsverfahren von Bruchgleichungen

Du kannst dir das auch so merken:Einfach jeden Nenner jeweils auf die andere Seite hinüber multiplizieren. Wie das konkret geht, wird gleich noch gezeigt.

Aber nun zurück zu unserer Aufgabe:

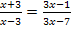
Erst verwenden wir noch das alte, allgemeine Verfahren, wie oben beschrieben, um daran zu zeigen, dass das Multiplizieren mit dem Hauptnenner hier dem kreuzweise Multiplizieren entspricht.

1. Definitionsmenge ermitteln:

Wir setzen die Nenner jeweils gleich Null und lösen nach x auf. So erhalten wir die Definitionslücken.

Die Definitionsmenge ist daher:D = ℚ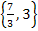

2. Hauptnenner aller Brüche bilden, die in der Gleichung vorkommen:

Der Hauptnenner ist hier einfach das Produkt der beiden Nenner, also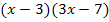

3. Mit dem Hauptnenner auf beiden Seiten der Gleichung multiplizieren, d.h. bei allen vorkommenden Brüchen jeweils den Zähler mit dem Hauptnenner multiplizieren

|

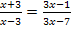
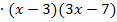
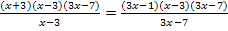
4. Soweit möglich kürzen    Gleichung, die kein x mehr im Nenner hat

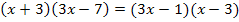
5. Diese Gleichung nach x auflösen

|

|

|

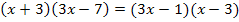
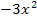
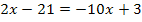
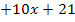
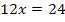
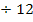
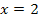
6. Kontrollieren, ob das Ergebnis in der Definitionsmenge enthalten ist (Wenn nicht, dann ist der berechnete Wert keine Lösung der Gleichung.)

Die Definitionsmenge ist D = ℚ 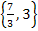. Der berechnete Wert x = 2 liegt also innerhalb der Definitionsmenge. x = 2 ist somit Lösung der Bruchgleichung.

7. Probe durchführen

Nur zur Sicherheit machen wir noch die Probe mit x = 2.

Hier noch einmal die angegebene Gleichung:

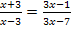
Probe für x = 2:

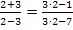
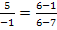
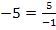
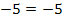(wahr)

Super! Das passt! Durch x = 2 ist die Gleichung erfüllt.

Das gerade vorgeführte allgemeine Verfahren zur Lösung von Bruchgleichungen ist leider sehr lang. Schneller geht es hier, wie oben schon erwähnt, durch das kreuzweise Multiplizieren. Probieren wir es doch ´mal an unserer Gleichung aus!

An Stelle der Schritte 2, 3 und 4 (2. Hauptnenner suchen, 3. damit multiplizieren und 4. kürzen) multiplizieren wir jetzt einfach kreuzweise:

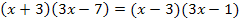
Das ist natürlich wieder die selbe Gleichung, die wir schon oben beim allgemeinen Verfahren erhalten haben. (Nur auf der rechten Seite der Gleichung sind die beiden Faktoren vertauscht, doch bei Produkten spielt das ja keine Rolle, denn es gilt: )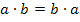

Das ist natürlich kein Zufall! Bei Gleichungen der Form 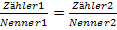kann immer an Stelle des Multiplizierens mit dem Hauptnenner und anschließendem Kürzens auch einfach kreuzweise multipliziert werden. In anderen Worten:Kreuzweise multiplizieren darfst du nur dann, wenn auf beiden Seiten der Gleichung jeweils ein einzelner Bruch steht. Ist dies nicht der Fall kannst du entweder mit dem Hauptnenner multiplizieren und kürzen (allgemeines Verfahren) oder die Gleichung zuerst so umformen, dass auf beiden Seiten jeweils ein einzelner Bruch entsteht, und danach kreuzweise multiplizieren. Das ist Geschmacksache!

---