Rechnerische Lösungsverfahren von Bruchgleichungen
6. Kontrollieren, ob das Ergebnis in der Definitionsmenge enthalten ist (Wenn nicht, dann ist der berechnete Wert keine Lösung der Gleichung.)
Die Definitionsmenge ist D = ℚ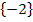 
. Der berechnete Wert x = – 4 liegt also innerhalb der Definitionsmenge. x = – 4 ist somit Lösung der Bruchgleichung.
7. Probe durchführen
Nur zur Sicherheit machen wir noch die Probe mit x = -4.
Hier noch einmal die angegebene Gleichung:
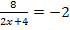
Probe mit x = -4: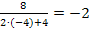 
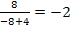
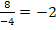
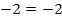(wahr)
Wunderbar! Jetzt wissen wir sicher, dass die Gleichung 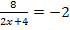durch x = – 4 erfüllt ist. Die Lösungsmenge war hier zwar nicht verlangt;wir geben sie trotzdem noch kurz an. Sie lautet:L =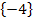 
Zugegeben, diese beiden Teilaufgaben waren echt noch recht leicht. Aber wir arbeiten uns lieber langsam an die schweren Aufgaben heran. Die schweren Aufgaben kommen schon noch. Die nächste Teilaufgabe ist schon ein klein wenig schwieriger. Doch sie lässt sich mit einem Verfahren, das man „kreuzweise Multiplizieren“ nennt, gut lösen. Das kreuzweise Multiplizieren lässt sich vom Multiplizieren mit dem Hauptnenner ableiten. Wie das geht, wirst du gleich sehen.
zu 1c.)
Hier noch einmal die Angabe: 
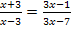
Lösung:
Zuerst werden wir diese Bruchgleichung nach dem oben beschriebenen allgemeinen Verfahren lösen, so wie wir es auch bei den vorherigen Teilaufgaben gemacht haben. Du wirst daran sehen, dass es bei dieser Gleichung jedoch auch einfacher geht. Man kann hier nämlich das sogenannte „kreuzweise Multiplizieren“ anwenden. Dieses Verfahren ergibt sich letztendlich durch das Multiplizieren mit dem Hauptnenner.
Diese Bruchgleichung hat die Form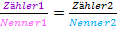 
;es steht also auf beiden Seiten der Gleichung jeweils ein einzelner Bruch. Nur bei solchen Gleichungen kannst du kreuzweise multiplizieren. Damit ist folgendes gemeint:
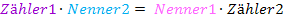
Und das Gleiche noch einmal völlig unmathematisch gesagt:Du sollst das, was in der Gleichung rechts unten steht, mit dem, was links oben steht, malnehmen bzw. das, was links unten steht, mit dem, was rechts oben steht, malnehmen. (Dazwischen steht dabei natürlich ein Gleichheitszeichen.) Sorry, das klingt jetzt fürchterlich kompliziert! Ich hoffe, dass ich dich jetzt nicht total verwirrt habe.
Also versuchen ich es noch einmal etwas einfacher zu sagen:Das von links unten kommt nach rechts oben und umgekehrt das von rechts unten nach links oben. Das heißt „kreuzweise multiplizieren“, weil man sich in der Mitte, wie oben gezeigt, ein Kreuz denken kann.
