Rechnerische Lösungsverfahren von Bruchgleichungen
Genauso wenig kann die Zahl 2 alleine der Hauptnenner sein, denn der Bruch 
ließe sich nicht auf den Nenner 2 bringen.
Auf den Nenner 2x lassen sich dagegen alle in der Gleichung vorkommenden Brüche (also , 
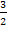und 
) bringen. 2x ist ja auch unser gesuchter Hauptnenner, also der Nenner, auf den man alle auftretenden Brüche bringen könnte.
Den Bruch würde man mit 2 erweitern, um ihn auf den Nenner 2x zu bringen: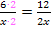 
Den Bruch 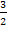würde man mit x erweitern, um ihn auf den Nenner 2x zu bringen: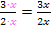 
Den Bruch würde man mit 2 erweitern, um ihn auf den Nenner 2x zu bringen: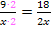 
Nun fragen viele Schüler, ob man nicht einfach alle auftretenden Nenner miteinander multipliziert als Hauptnenner verwenden kann. Manchmal stimmt das, aber eben nicht immer, denn der Hauptnenner soll ja das kleinste gemeinsame Vielfache sein! In diesem Fall ist ja auch nicht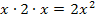 
der Hauptnenner, sondern nur 2x. Es würden sich zwar auch alle auftretenden Brüche auf den Nenner 
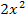erweitern lassen, doch bekommt man damit viel zu große Potenzen, mit denen es sich schlecht rechnen lässt.
Da es für viele Schüler anfangs oft schwierig ist den Hauptnenner selbst zu finden, werden wir in späteren Aufgaben noch genauer darauf eingehen.
Nun müssen wir die ganze Gleichung mit dem Hauptnenner, also mit 2x, multiplizieren. Es wird also auf beiden Seiten mit 2x multipliziert. Wir machen das im Folgenden extrem ausführlich. Wenn du alleine rechnest, brauchst du nicht alle Zwischenschritte aufschreiben. Das wird bei diesem ersten Beispiel nur so ausführlich gezeigt, damit du wirklich alles gut nachvollziehen kannst.
| 
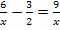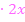
Beide Seiten der Gleichung komplett mit dem Hauptnenner multiplizieren:
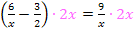
Klammer auflösen, d.h. jeden einzelnen Bruch mit dem Hauptnenner multiplizieren:
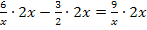
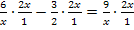
Also, einfach den Zähler der einzelnen Brüche mit dem Hauptnenner multiplizieren:
Kürzen:
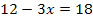
Nun liegt eine einfache lineare Gleichung vor, die wir nur noch nach x auflösen müssen. Das dürfte ja kein Problem mehr für dich darstellen.
| 
| 
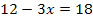
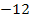
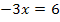
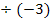
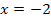
Der berechnete Wert liegt innerhalb der Definitionsmenge D = ℚ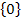 
. Daher lautet die Lösungsmenge:L =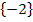 
Zur Sicherheit solltest du jedoch auch immer die Probe mache, also den berechneten Wert für x in die angegebene Gleichung einsetzen und kontrollieren, ob sich eine wahre Aussage ergibt.
Hier noch einmal die gegebene Gleichung: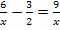
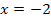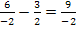
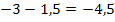
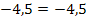
Probe für : 
(wahr)
Super!
