Rechnerische Lösungsverfahren von Bruchgleichungen

|

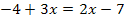
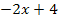
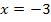
Es kommt natürlich wieder das gleiche Ergebnis heraus wie schon oben. Doch ging es so viel schneller. Auf diesem Weg mussten wir auch keine quadratische Gleichung lösen. Wenn du nicht selbst auf diese Idee gekommen bist, ist das nicht schlimm. Das Kreuzweise Multiplizieren klappt ja auch. Doch solltest du einfach ´mal sehen, dass es auch schneller geht, wenn man auf beiden Seiten der Gleichung den selben Nenner hat oder schnell herstellen kann.

zu 4b.)

Hier noch einmal die Angabe:

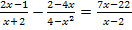
Lösung:

Beim Nenner des zweiten Bruchs handelt es sich um die dritte Binomische Formel. Wir formen diesen Nenner in Produkt um:

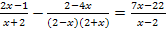
Definitionsmenge:      D = ℝ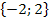

Es fällt dir bestimmt auf, dass  die Faktoren 2 – x und x – 2 bis auf ihre Reihenfolge gleich sind. Wir klammern -1 bei dem Faktor 2 – x aus, um die Reihenfolge umzudrehen. Bei einer Summe spielt die Reihenfolge keine Rolle, so dass 2 + x das Gleiche ist wie x + 2. Hier kann die Reihenfolge einfach umgedreht werden.

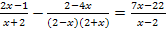
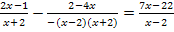
Wir ziehen das Minuszeichen aus dem Nenner vor den Bruch. Wegen 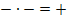ergibt sich dann ein Plus vor dem zweiten Bruch.

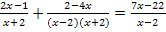
Nun kann mit dem Hauptnenner 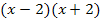multipliziert werden:

|

|

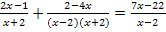
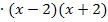
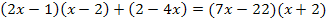
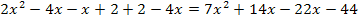
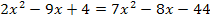
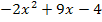
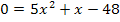
Vor 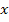steht eigentlich die Zahl 1;daher gilt:a = 5, b = 1, c = -48

Eingesetzt in die Mitternachtsformel ergibt das:

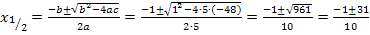
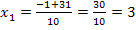
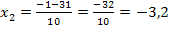
Beide Werte liegen in der Definitionsmenge D = ℝ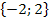

Probe für 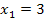(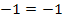wahr)

Probe für 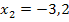(wahr)

Lösungsmenge:L =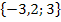

zu 4c.)

Hier noch einmal die Angabe:

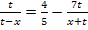
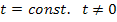
Lösung:

Hier tritt nun ein neues Problem auf:In der Gleichung kommt neben der Lösungsvariablen x auch noch der zweite Buchstabe t vor. t ist ein sogenannter Parameter. Das ist im Gegensatz zu x eine Konstante, d.h. eine feste Zahl. Das erkennt man in dieser Aufgabe an der Angabe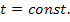

Man soll also, wie auch bei den vorherigen Aufgaben, nach x auflösen, weil x die Lösungsvariable ist. Die Lösung wird dabei noch den Parameter t enthalten. Man muss also in Abhängigkeit von t rechnen. Das bedeutet, dass man so rechnen soll, als wäre t eine konkrete Zahl.

Auch die Definitionsmenge muss in Abhängigkeit von t angegeben werden:   D = ℝ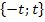

Tipp:Wenn dir das t Schwierigkeiten macht, denkst du dir einfach:  „t ist bloßeine Zahl. Wie würde ich denn rechnen, wenn t beispielsweise 3 wäre.“ Natürlich darfst du nicht wirklich die Zahl 3 oder irgendeine andere Zahl für t einsetzen. Nur denken sollst du dir das! Du musst also schon mit t rechnen, ohne wirklich etwas einzusetzen.

Wir bringen die rechte Seite auf einen gemeinsamen Nenner, damit wir dann kreuzweise multiplizieren können.

|

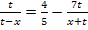
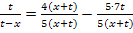
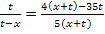
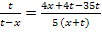
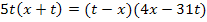
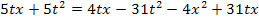
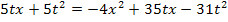
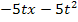
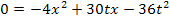
Wir hätten natürlich auch unser 1. Verfahren anwenden können. Indem man die ursprünglich gegebene Bruchgleichung direkt mit dem Hauptnenner multipliziert, kürzt und soweit möglich zusammenfasst, kommt man wieder auf die selbe Gleichung:

|

|

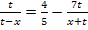
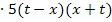
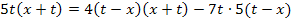
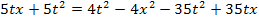
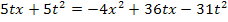
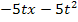
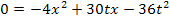
Wir setzen in die Mitternachtsformel ein:

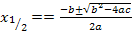
(Mitternachtsformel)

Dabei gilt:a = -4, b = 30t, c =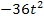

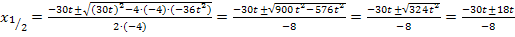
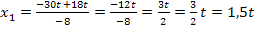
Beide Werte liegen innerhalb der Definitionsmenge D = ℝ 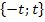. Daher si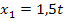nd und 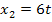die Lösungen der Bruchgleichung.

Strenggenommen hätten wir erst noch die Probe machen müssen also die berechneten Wert für x (und nicht etwa für t) in die ursprüngliche Gleichung einsetzen. Hier geht es leider nicht mit dem Taschenrechner!

Hier noch einmal die Angabe:

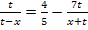
Probe für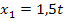

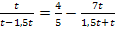
Ab hier geht es natürlich auch mit dem Taschenrechner: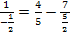     

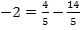
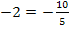
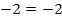(wahr)

Probe für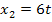

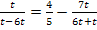
Ab hier geht es natürlich auch mit dem Taschenrechner: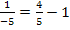     

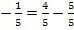
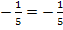(wahr)

Das war´s zum Thema „Bruchgleichungen rechnerisch lösen“. Du hast nun gesehen, wie man Bruchgleichungen lösen kann. Dass es dabei meist verschiedene Rechenwege gibt, die alle mehr oder weniger gut klappen, macht es für den Schüler sicher nicht leichter. Optimal wäre es, wenn du je nach Aufgabe selbst erkennen kannst, welches Verfahren jeweils das geschickteste ist. Das braucht aber etwas Erfahrung, sprich Übung. Für den Anfang reicht es meist aus, eines (oder evtl.  zwei) der Verfahren wirklich sicher zu beherrschen und damit dann immer zu rechnen. Besser du kannst nur eines der drei Verfahren absolut sicher, als dass du alle drei ein bisschen kannst, aber keines richtig!

---