Rechnerische Lösungsverfahren von Bruchgleichungen
| 
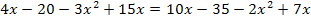
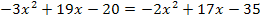
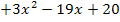
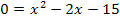
Es liegt nun eine gemischtquadratische Gleichung, also eine Gleichung mit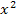 
und x, vor. Wir lösen sie mit der Mitternachtsformel.
Zur Erinnerung:
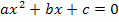
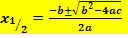(Mitternachtsformel)
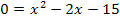
Vor 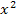steht eigentlich die Zahl 1;daher gilt:a = 1, b = -2, c = -15
Eingesetzt in die Mitternachtsformel ergibt das:
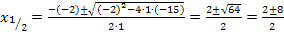
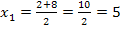
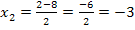
Was fällt dir nun auf? Klar,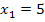 
liegt nicht in der Definitionsmenge D = ℝ 
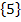und kann somit keine Lösung der Gleichung sein. Für x = 5 wird ja der Nenner Null! Also bleibt als einzige Lösung 
.
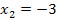Lösungsmenge:L =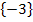 
Hier noch einmal die Gleichung: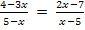 
So, nun war am Anfang der Aufgabe von einem Trick die Rede. Hast du eine Idee, wie sich diese Aufgabe viel schneller hätte lösen lassen?
Nein? Dann betrachte doch ´mal die beiden Nenner. Was fällt dir dabei auf?
Richtig;es ist nur die Reihenfolge umgekehrt! Sonst sehen die beiden Nenner gleich aus. Aber was bringt uns diese Erkenntnis jetzt? Ganz einfach:Wir klammern bei einem der beiden Nenner -1, also ein Minuszeichen, aus. Dadurch dreht sich dann die Reihenfolge dieses Nenners um. Zieht man dann noch das Minus vor den Bruchstrich sind beide Nenner gleich und man kann nur die beiden Zähler gleichsetzen.
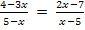
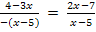
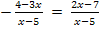
Multiplikation mit dem Hauptnenner x – 5 ergibt:
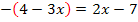
Vorsicht:Minus vor dem Bruch: Klammer nicht vergessen!
