Rechnerische Lösungsverfahren von Bruchgleichungen
Eingesetzt in die Mitternachtsformel ergibt das:
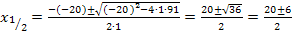
Nun wissen wir, dass der Nenner 
für x = 13 und für x = 7 Null ergibt. Weil du nun die Lösungen der Gleichung 
kennst, kannst du den Nenner jetzt auch leicht faktorisieren, also als Produkt schreiben. Wenn man weiß, wie das geht ist es wirklich einfach. Doch wie geht das denn nun?
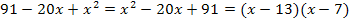
Du musst bei den Lösungen der Gleichung , also bei den Zahlen 13 und 7, nur die Vorzeichen umdrehen, um auf die Zahlen in den Klammern zu kommen.
Anmerkung:Steht vor der höchsten Potenz von x, also vor dem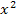 
, noch eine Zahl, muss beim Faktorisieren diese Zahl vor die Klammern geschrieben werden. Vergisst man das, ist die Faktorisierung falsch! Genaueres dazu unter Faktorisieren!
Dass die beiden Brüche 
und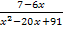 
wirklich äquivalent (gleich) sind, kannst du selbst leicht überprüfen:Wenn du die beiden Klammern im Nenner des einen Bruchs ausmultiplizierst, kommst du auf den anderen Bruch. Das ist nicht weiter schwer.
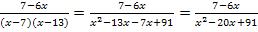
Der Bruch 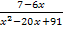lautet daher in seiner faktorisierten Form:
Damit können wir unsere Gleichung auch in der folgenden Form schreiben:
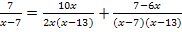
Neben den Werten 7 und 13 gibt es noch eine weitere Definitionslücke bei x = 0, weil auch für x = 0 der Nenner des mittleren Bruchs Null ergibt. Es existieren somit die drei Definitionslücken x = 0, x = 7 und x = 13. Die Definitionsmenge bezüglich der Grundmenge G = ℚ(vergleiche Angabe!) lautet daher:
D = ℚ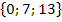 
Wir kürzen noch beim mittleren Bruch mit 2x:
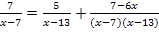
Jetzt sieht das Ganze schon nicht mehr so schlimm aus und es geht wieder ganz normal weiter:Wir multiplizieren mit dem Hauptnenner, also mit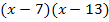 
.
| 
| 
| 
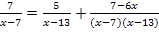
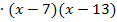
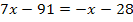
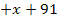
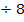
liegt in der Definitionsmenge
Probe:8 = 8 (wahr)
Lösungsmenge:L = 
Bisher haben wir nur Bruchgleichungen behandelt, bei denen am Schluss eine lineare Gleichung heraus kam. Bisher ist 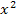also immer weggefallen. Dass das nicht immer so sein muss, wirst du gleich an den folgenden Aufgaben sehen. Ab der 9. Klasse können auch Bruchgleichungen kommen, die zu Quadratischen Gleichungen führen.
4. Bsp.: Löse die folgenden Gleichungen soweit möglich!
a.)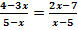 
b.)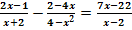 
c.) 
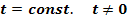
Lösung:
zu 4a.)
Definitionsmenge:D = ℝ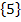 
Man kann diese Aufgabe entweder durch kreuzweises Multiplizieren lösen oder mit einem kleinen algebraischen Trick. Zuerst gehen wir den Standartweg und multiplizieren kreuzweise. Das ist vermutlich auch der Weg, den du eingeschlagen hättest.
