Rechnerische Lösungsverfahren von Bruchgleichungen
Damit du diese Aufgabe lösen kannst, musst du die Binomischen Formelnschon gelernt haben. Die Binomischen Formeln sind aber erst Stoff der 9. Klasse. Gehe direkt zu 3e.). Diese Aufgabe kann auch von Schülern der 8. Klasse gelöst werden.
zu 3d.)
Lösung:
Hier noch einmal die Angabe:
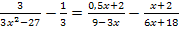
Ausklammern: 
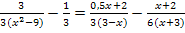
3. Binomische Formel anwenden: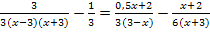 
Im dritten Nenner -1 ausklammern: 
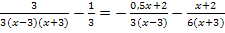
Definitionsmenge: D = ℚ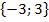 
Hinweis:
In der Aufgabenstellung war die Grundmenge mit G = ℚ angegeben. Ab der 9. Klasse gilt aber in den meisten Aufgaben G = ℝ. Dann wäre die Definitionsmenge: D = ℝ
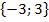
Mit dem Hauptnenner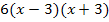 
multiplizieren und kürzen:
| 
| 
| 
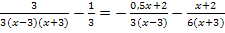
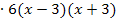
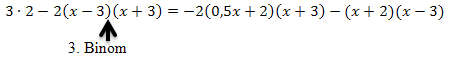
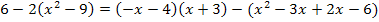
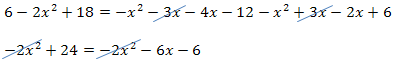
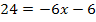
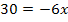
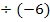
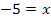
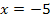liegt in D = ℚ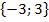
Hier noch einmal die Angabe:
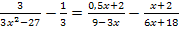
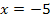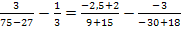
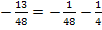
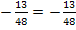
Probe für : 
(wahr)
Lösungsmenge:L =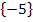 
zu 3e.)
Hier noch einmal die Angabe: 
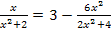
Ausklammern: 
Mit 2 im letzten Bruch kürzen: 
Definitionsmenge:D = ℚ (Der Nenner kann hier gar nicht Null ergeben. Daher kann für x alle Werte aus der Grundmenge G = ℚ einsetzen.)
Mit dem Hauptnenner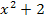 
multiplizieren und kürzen:
| 
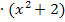
liegt in D = ℚ
Probe: 
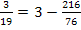
(wahr)
Lösungsmenge:L =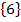 
Für Schüler der 8. Klasse ist hier Schluss! Das waren hoffentlich genug Beispiele zur rechnerischen Lösung von Bruchgleichungen.
Der restliche Teil dieses Kapitels ist nur noch etwas für Schüler ab der 9. Klasse.
zu 3f.)
Hier noch einmal die Gleichung: 
Lösung:
Hier muss erst einmal der Nenner jedes einzelnen Bruchs faktorisiert, also als Produkt geschrieben werden, damit wir die Definitionsmenge und später den Hauptnenner finden können.
Beim mittleren Bruch lässt sich im Nenner ausklammern. Probleme bereitet aber der Nenner des letzten Bruchs.
Wir klammern erst ´mal aus: 
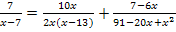
Um den Nenner des letzten Bruchs zu faktorisieren, setzen wir ihn gleich Null. (So erhalten wir auch gleich die ersten Definitionslücken.) Dabei müssen wir eine gemischtquadratische Gleichung lösen, also eine Gleichung mit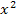 
und x. Wir verwenden die Mitternachtsformel. (Ausführliche Erklärungen, wie man quadratische Gleichungen lösen kann, findest du im Kapitel Quadratische Gleichungen.)
Zur Erinnerung:
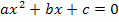
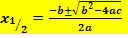(Mitternachtsformel)
a steht immer für die Zahl vor dem 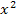, b entsprechend für die Zahl vor dem x und c für die Zahl ohne x.
Vor 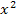steht eigentlich die Zahl 1;daher gilt:a = 1, b = – 20, c = 91
