Rechnerische Lösungsverfahren von Bruchgleichungen
Inzwischen müsstest du die Vorgehensweisen bei den einzelnen Verfahren soweit verstanden haben, dass du keine ausführlicheren Erklärungen zu den einzelnen Schritten mehr brauchst. Daher wird ab sofort auf die Erklärungen in Worten (außer in besonderen Ausnahmefällen) verzichtet und nur noch die Rechnung gezeigt.
zu 3c.)
Hier noch einmal die Angabe:
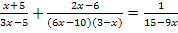
Lösung:
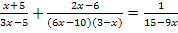
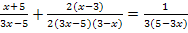
Nebenrechnung zur Ermittlung der Definitionsmenge:
| 
| 
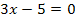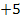
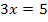
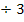
Definitionsmenge: D = ℚ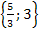 
Im Folgenden wird ein kleiner algebraischer Trick angewendet, um bei einer Differenz die Reihenfolge umzudrehen:-1 (d.h. ein Minuszeichen) ausklammern
Dieser Trick wird ausführlich im Kapitel Definitionsmenge einer Bruchgleichung im Bsp. 1c.) erläutert. Falls du das mit dem Minus-Ausklammern nicht kennst, solltest du dir das unbedingt gut anschauen! Den Trick kann man nämlich oft brauchen.
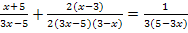
Es fällt dir sicher auf, dass einmal der Faktor 3x – 5 und einmal genau der umgekehrte Faktor 5 – 3x auftaucht. Das Selbe ist es bei x – 3 und 3 – x im zweiten Bruch. Wir wollen jeweils bei einem der beiden Faktoren die Reihenfolge umdrehen. Da der Faktor 3x – 5 zweimal auftritt, aber der umgekehrte Faktor 5 – 3x nur einmal, wollen wir bei letzterem die Reihen folge umdrehen. Bei den Faktoren x – 3 und 3 – x ist es egal, bei welchem wir -1 ausklammern und somit die Reihenfolge umdrehen. Jeder der beiden kommt ja nur einmal vor.
Um nun die Reihenfolge von 5 – 3x im Nenner des letzten Bruchs umzudrehen wird -1, also ein Minuszeichen, ausgeklammert! Das bietet sich eben an, da in den anderen beiden Brüchen schon der Faktor 3x – 5 im Nenner vorkommt. Ebenso wird im Zähler des zweiten Bruchs -1 ausgeklammert, damit sich die Reihenfolge des Faktors x – 3 umdreht. Dann lässt sich zusätzlich zu der Zahl 2 im zweiten Bruch nämlich auch 3 – x kürzen.
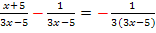
Wir verwenden das 1. Verfahren:Multiplizieren mit dem Hauptnenner
Hauptnenner: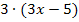 
| 
|
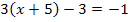
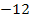
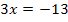
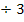
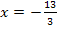
Der berechnete Wert liegt in der Definitionsmenge.
Hier noch einmal die Angabe:
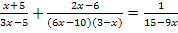
Probe für :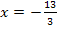 
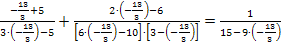
Mit dem Taschenrechner: 
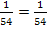
(wahr)
Lösungsmenge:L =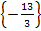 
Hinweis:
Man hätte auch folgendermaßen vorgehen können:
| 
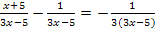
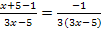
Nicht die Klammern ausmultiplizieren! Sonst bekommst du eine quadratische Gleichung, also eine Gleichung mit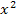 
! Besser du teilst durch (3x – 5), wie hier vorgeführt!
|
|
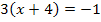
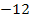
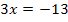
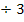
Die Teilaufgabe 3d.) ist nicht für Schüler der 8. Klasse geeignet!
