Rechnerische Lösungsverfahren von Bruchgleichungen

Du musst zugeben, es geht viel schneller, wenn man die Klammern vorher nicht erst ausmultipliziert, sondern direkt durch den Faktor 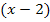dividiert.

Tipp:

Immer wenn auf beiden Seiten einer Gleichung ein Produkt vorliegt und ein einzelner Faktor auf beiden Seiten vorkommt, man ihn also durch Division beseitigen kann, solltest du immer durch diesen Faktor teilen und eben nicht ausmultiplizieren.

3. Verfahren: Alles zuerst auf den Hauptnenner bringen und dann nur noch die Zähler gleichsetzen

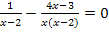
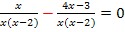
Achtung:Minus vor dem Bruch: Vergiss die Klammer um 4x – 1 nicht!

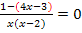
Jetzt müssten eigentlich die Zähler der linken und rechten Seite gleichgesetzt werden. Aber auf der rechten Seite steht ja gar kein Bruch! Entweder denkst du dir an Stelle der Zahl 0 auf der rechten Seite einfach irgendeinen Bruch mit 0 im Zähler, z. B. 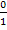. Dann kannst du wieder die Zähler gleichsetzen. Oder du bringst den Nenner der linken Seite auf die rechte Seite, indem du mit ihm multiplizierst. Wir nehmen die letzte Variante.

|

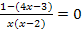
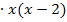
So, was kommt da denn nun heraus?

Falsch wäre auf jeden Fall:

Warum? Ganz einfach: 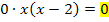und nicht etwa !!!

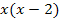würde sich nämlich aus der folgenden Gleichung ergeben:

|

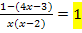
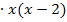
Bei unserer Gleichung steht aber auf der rechten Seite eine Null und keine Eins!

Daraus folgt nun für unsere Gleichung:

|

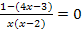
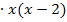
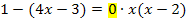
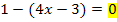
Es handelte sich hierbei um einen wichtigen Sonderfall einer Bruchgleichung. Wir mussten ja die Gleichung 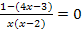lösen. D.h. es war die Frage zu beantworten, wann der Bruch 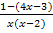Null ergibt. Allgemein stellt sich also die Frage:Wann ist ein Bruch gleich Null? Oder etwas mathematischer geschrieben: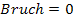       

|

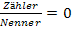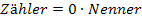
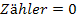
Du kannst an der obigen Rechnung sehen, dass man nur den Zähler des Bruchs gleich Null setzen muss, damit der ganze Bruch Null ergibt. Der Nenner fällt wegen 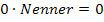einfach komplett weg!

Merke:Ein Bruch ist gleich Null, wenn der Zähler gleich Null ist!

Damit lässt sich unsere Gleichung ganz einfach lösen:

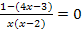
(Bruch = 0)

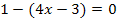(Zähler = 0)

Der Rest der Aufgabe stellt kein Problem mehr dar:

|

|

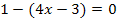
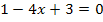
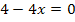
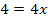
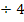
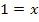
Wir müssten noch kontrollieren, ob x = 1 in der Definitionsmenge liegt, und dann noch die Probe machen, doch das haben wir ja alles bereits oben beim 1.Verfahren gemacht.

Wir stellen die drei Verfahren noch einmal direkt gegenüber. Dabei beginnen wir mit der gekürzten Form der Gleichung.

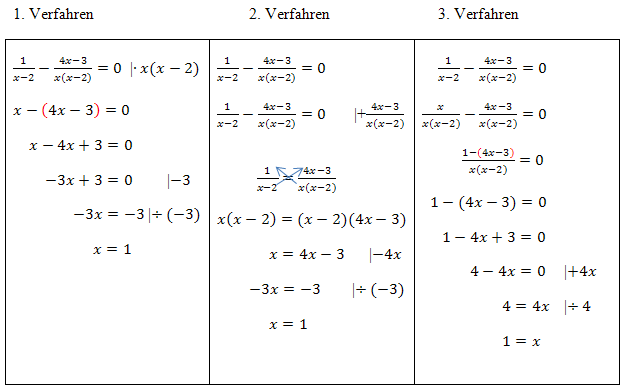
Nun kannst du dir hoffentlich den Weg, der für dich am besten geeigneten ist, leichter heraussuchen.

---