Rechnerische Lösungsverfahren von Bruchgleichungen

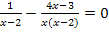
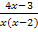
|+ D = ℚ

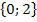
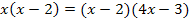
So, nun rechne erst einmal alleine weiter! Was für ein Problem tritt dann auf?

Du wirst vermutlich die Klammern ausmultipliziert haben. Dann hast du folgendes erhalten:

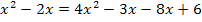
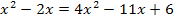
Nun müsstest du bemerkt haben, dass das x mit dem Quadrat nicht herausfällt. Für Schüler der 8. Klasse ist das so noch nicht lösbar. (Ab der 9. Klasse könnte die Mitternachtsformel zur Lösung dieser quadratischen Gleichung verwendet werden. Das ist zwar aufwendig, führt aber wenigstens zur Lösung.) Was machen jetzt aber Schüler der 8. Klasse? „Das kann ich noch nicht! Das haben wir noch nicht gelernt!“ kann man hier nicht gelten lassen. Du hast ja gesehen, dass du die Gleichung zumindest mit dem 1. Verfahren doch schon lösen kannst. Auch in der 8. Klasse musst du diese Aufgabe  lösen können. Aber geht das mit kreuzweisem Multiplizieren vielleicht gar nicht? Doch!

Wir machen einfach folgendes:Wir multiplizieren die Klammern erst gar nicht aus, sondern dividieren auf beiden Seiten der Gleichung durch den Faktor 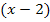. Das ist innerhalb der Definitionsmenge D = ℚ 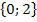eine Äquivalenzumformung. Man darf also in der Definitionsmenge durch den Faktor 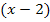auf beiden Seiten teilen. Warum ist das mit der Definitionsmenge hier überhaupt wichtig? Du weißt, dass man durch Null nicht dividieren darf. Der Faktor 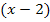würde aber Null ergeben, wenn man für x den Wert 2 einsetzt. Das bedeutet für x = 2 dürfen wir nicht durch 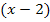teilen, weil dann die Division nicht definiert wäre. Die Zahl 2 ist aber sowieso nicht in der Definitionsmenge enthalten. Das bedeutet, dass wir innerhalb der Definitionsmenge ohne Probleme durch den Faktor 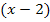dividieren können. Dadurch fällt die Klammer 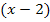auf beiden Seiten der Gleichung weg.

|

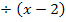
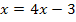
Diese Gleichung enthält kein x mit Quadrat und du kannst sie ganz leicht nach x auflösen.

|

|

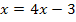
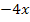
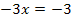
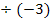
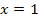
Es kommt natürlich die selbe Lösung heraus wie oben. (Probe und Lösungsmenge sparen wir uns. Das haben wir oben schon gemacht.)

Hinweis für Schüler ab der  9. Klasse:

Wenn du die Klammern doch ausmultipliziert hättest, weil du nicht auf die Idee gekommen bist, durch den Faktor 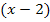zu teilen, wäre es mit Hilfe der Mitternachtsformel folgendermaßen weitergegangen:

|

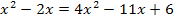
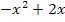
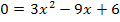
Einsetzen von a = 3, b = -9 und c = 6  in die Mitternachtsformel ergibt:

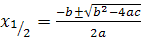
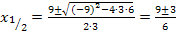
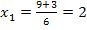
Vorsicht: 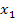liegt nicht in der Definitionsmenge D = ℚ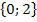

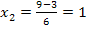
Nur 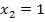kann Lösung der Gleichung sein, weil nur 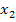in der Definitionsmenge enthalten ist. Dann müsste man noch die Probe für x = 1 machen und die Lösungsmenge angeben. Dann wäre man endlich fertig. Das hätte also auch funktioniert, ist jedoch sehr umständlich!

---