Rechnerische Lösungsverfahren von Bruchgleichungen
2. Verfahren:
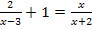
![]() D = ℚ
D = ℚ 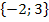
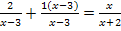
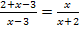
![]()
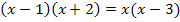
![]() Achtung:Klammern nicht vergessen!
Achtung:Klammern nicht vergessen!
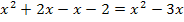
![]() |
| 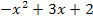
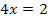
![]() |
| 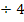
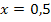
Natürlich ist wieder das Selbe wie oben herausgekommen. Die Probe und die Angabe der Lösungsmenge sparen wir uns jetzt aber dann doch;das steht ja alles schon oben.
Und jetzt noch ein drittes Mal. Jetzt verwenden wir das 3. Verfahren:Alles so erweitern, dass alles den gleichen Nenner hat. Dann Nenner weglassen, also nur noch die Zähler gleichsetzen.
3. Verfahren:
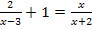
![]() D = ℚ
D = ℚ 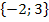
Hauptnenner: 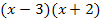
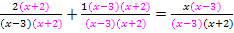
Nenner weglassen. (Eigentlich ist das ja nichts anderes als mit dem Hauptnenner zu multiplizieren und dann zu kürzen.)
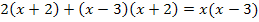
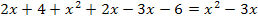
![]() |
| 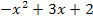
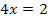
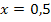
Dass wieder x = 0,5 herauskommt, war ja klar. Es ging ja aber um den Rechenweg. Probe und Lösungsmenge schreiben wir nicht noch einmal auf.
zu 3b.)
Erst noch einmal die Angabe:![]()
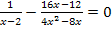
Lösung:
Ausklammern ergibt:![]()
![]()
![]() D = ℚ
D = ℚ 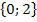
Vereinfachen durch Kürzen:![]()
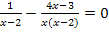
Wir fangen wieder mit dem 1. Verfahren an, obwohl sich hier eher eine andere Methode anbietet. Was würdest du denn bei dieser Aufgabe nehmen? Am einfachsten scheint hier wohl die 2. Methode sein, d.h. Gleichung auf die Form 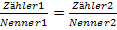 bringen und dann kreuzweise multiplizieren. Doch dabei tritt ein Problem auf. Du wirst es gleich sehen.
bringen und dann kreuzweise multiplizieren. Doch dabei tritt ein Problem auf. Du wirst es gleich sehen.
Es werden im Folgenden wieder alle drei möglichen Lösungsverfahren an dieser Gleichung vorgeführt. Das hilft dir hoffentlich, den für dich besten Weg herauszufinden. Allerdings werden nun schon einige Zwischenschritte übersprungen. In Schulaufgaben hast du ja auch nicht die Zeit alle Zwischenschritte hinzuschreiben. Die wirklich wichtigen Schritte sind aber trotzdem alle gezeigt. (Kürzer sollte deine Lösung in Prüfungen nicht aussehen.)
1. Verfahren:Mit dem Hauptnenner multiplizieren
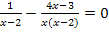
![]() |
| 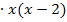
Vorsicht:Die Klammer um 4x – 3 nicht vergessen, wegen des Minuszeichens vor dem Bruch! Beachte:Ein Bruch wirkt immer wie eine Klammer. Daher bezieht sich das Minuszeichen vor dem zweiten Bruch auf den ganzen Bruch. Wenn mit dem Hauptnenner multipliziert und dann gekürzt wird, muss daher unbedingt eine Klammer gesetzt werden. Diese Klammer wird sehr oft vergessen. Also immer extrem aufpassen, wenn ein Minus vor einem Bruch steht.
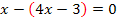
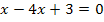
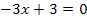
![]() |
| 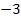
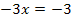
![]() |
| 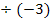
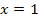
Der berechnete Wert liegt in der Definitionsmenge D = ℚ 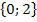 . Also noch schnell die Probe:
. Also noch schnell die Probe:
Hier noch `mal die Angabe: 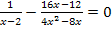
Probe für 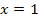
![]()
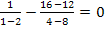
![]()
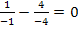
![]()
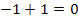
![]()
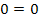
![]() (wahr)
(wahr)
Lösungsmenge L = 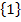
2. Verfahren: Gleichung auf die Form 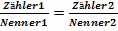 bringen und dann kreuzweise multiplizieren.
bringen und dann kreuzweise multiplizieren.

