Rechnerische Lösungsverfahren von Bruchgleichungen

Dieses Kapitel ist so aufgebaut, dass die ersten Aufgabenbeispiele auch von Schülern der 8. Klasse bearbeitet werden können. Sie führen immer zu linearen Gleichungen, also Gleichungen ohne 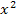. Das ist der größte Teil dieses Kapitels. Erst die Aufgaben gegen Ende sind nur für Schüler ab der 9. Klasse (G8 oder R6 mathematischer Zweig) geeignet, also nur für Schüler, die im Unterricht bereits gelernt haben, wie man gemischtquadratische Gleichungen löst. Dieser Teil ist aber extra gekennzeichnet.

Es gibt verschiedene Methoden, wie man Bruchgleichungen rechnerisch lösen kann. Das grundlegende Verfahren funktioniert folgendermaßen:

Merke:

Jede Bruchgleichung kann rechnerisch gelöst werden, indem man mit dem Hauptnenner multipliziert.

Damit du das besser verstehst, schauen wir uns jetzt gleich ein paar Beispiele unterschiedlichen Schwierigkeitsgrades an:

1. Bsp.:

Berechne die Lösungen der folgenden Bruchgleichungen in der Grundmenge G = ℚ!

a.)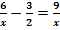       

b.)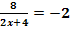       

c.)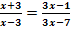       

d.)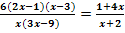       

e.)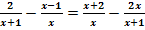       

f.)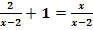       

Lösung:

zu 1a)

Hier noch einmal die Angabe:

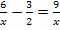
Zuerst geben wir die Definitionsmenge an:  D = ℚ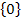

Für x darf hier nicht Null eingesetzt werden, da sonst der Nenner des ersten und dritten Bruchs gleich Null wird.

Nun wollen wir die Gleichung nach x auflösen. Dazu benötigen wir den Hauptnenner der gesamten Gleichung, also den gemeinsamen Nenner aller in der Gleichung vorkommenden Brüche. In diesem Fall ist es kein Problem den Hauptnenner zu finden. Er ist hier 2x, was dir hoffentlich klar ist. Der Hauptnenner ist ja immer das kleinste gemeinsame Vielfache aller Nenner, die in der Gleichung auftreten, also hier das kleinste gemeinsame Vielfache von x und von 2. Wir wollen das hier zwar nicht machen, aber es müssten sich alle vorkommenden Brüche so Erweitern lassen, dass sie dann einen gemeinsamen Nenner hätten. Dieser gemeinsame Nenner ist eben der sogenannte Hauptnenner. Jeder einzelne Nenner, der in der Gleichung vorkommt, muss sich auf den Hauptnenner erweitern lassen. Geht das nicht, dann war es auch nicht der Hauptnenner!

Zur Erinnerung:Erweitern darf man nur durch Multiplizieren, nicht aber mit Plus oder Minus!

Der Hauptnenner kann hier beispielsweise nicht einfach x sein, denn wie sollte man denn den Bruch 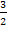erweitern, dass im Nenner x steht? Das geht ja gar nicht! Deshalb kann x auch nicht der Hauptnenner sein.

---