Rechnerische Lösungsverfahren von Bruchgleichungen

2. Verfahren:

|

|

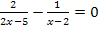
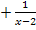
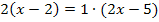
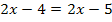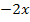
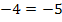(Widerspruch!)

Wir kommen natürlich wieder zu dem Ergebnis, dass die Lösungsmenge leer ist. Wundere dich bitte nicht darüber, dass vorher am Ende 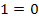herauskam und nun 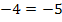. Man könnte die  -5 einfach auf die linke Seite bringen, dann würde man wieder 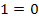erhalten. Doch diese Umformung ist ja gar nicht mehr nötig, denn man erkennt auch so, dass ein Widerspruch vorliegt.

Weil bekanntlich nur Übung den Meister macht:Gleich noch ein paar Aufgaben, natürlich wieder mit Lösung. Wichtig ist, dass du mit der Zeit ein Gefühl dafür bekommst, welches Verfahren bei welcher Aufgabe am besten funktioniert, und was dir am besten liegt.

3. Bsp.:

Ermittle die Lösungsmenge der folgenden Bruchgleichungen bezüglich der Grundmenge G = ℚ !

a.)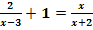       

b.)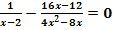       

c.)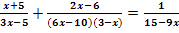       

d.) 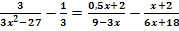       (Nur für Schüler ab der 9. Klasse!)

e.)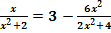       

f.) 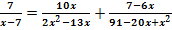       (Nur für Schüler ab der 9. Klasse!)

Hinweis:

Wie man die Definitionsmengen genau dieser Bruchgleichungen ermittelt, wurde schon im Kapitel Definitionsmenge von Bruchgleichungen im 1. Bsp. ausführlich erläutert. Daher wird die Definitionsmenge hier immer nur kurz angegeben, aber nicht näher darauf eingegangen, wie man darauf gekommen ist. Wenn du Fragen zur Definitionsmenge einer dieser Teilaufgaben hast, schaust du einfach im Kapitel Definitionsmenge von Bruchgleichungen im 1. Bsp. nach. Dort findest du genau die selben Gleichungen und die Erklärungen zu den jeweiligen Definitionsmengen. An dieser Stelle sollen jedoch das Augenmerk vor allem auf die verschiedenen rechnerischen Lösungswege gelegt werden.

zu 3a.)

Hier noch einmal die Angabe:

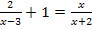
Lösung:

Definitionsmenge:      D = ℚ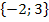

Es werden im Folgenden alle drei möglichen Lösungsverfahren an dieser Gleichung vorgeführt. Das hilft dir hoffentlich, den für dich besten Weg herauszufinden.

1. Verfahren:Mit dem Hauptnenner multiplizieren und kürzen. Diese beiden Schritte könnten gleich im Kopf gemacht werden. Somit könnte die zweite Zeile der folgenden Rechnung auch übersprungen werden. (Bei den Teilaufgaben b.) bis f.) wird die entsprechende Zeile nicht mehr gezeigt werden. Die meisten Lehrer überspringen diesen Schritt ebenfalls.)

|

|

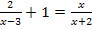
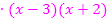
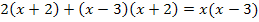
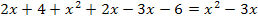
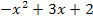
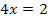
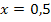
Der berechnete Wert liegt in der Definitionsmenge D = ℚ .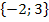

Nur noch schnell die Probe:

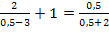
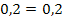(wahr)

Lösungsmenge:L =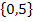

Nun das Ganze noch einmal von vorne, jetzt aber mit dem 2. Verfahren:Gleichung auf die Form 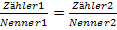bringen, also hier nur noch die linke Seite der Gleichung auf einen gemeinsamen Nenner bringen, und dann kreuzweise multiplizieren.

---