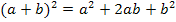Rechnerische Lösungsverfahren von Bruchgleichungen
1. Nenner: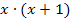 
2. Nenner: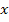 
3. Nenner: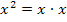 
4. Nenner: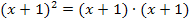 
Es treten hier keine reinen Zahlen als einzelne Faktoren auf. Daher müssen wir keine Primfaktorzerlegung machen. Es treten nur die Faktoren x und x + 1 auf. Wir überlegen uns nun, mit welcher Potenz wir diese beiden Faktoren jeweils im Hauptnenner brauchen.
Fangen wir ´mal mit dem Faktor x an. Nun schaust du, in welchem Nenner der Faktor x am häufigsten auftritt, also mit der höchsten Potenz. Du erkennst, dass hier im 3. Nenner der Faktor x zweimal vorkommt, also mit dem Exponenten 2. In den anderen Nennern kommt x nur einmal, also mit dem Exponenten 1 oder gar nicht vor. Daher ist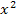 
die höchste Potenz, die vorkommt. Im Hauptnenner brauchen wir also den Faktor .
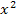Jetzt machen wir das genauso mit dem zweiten Faktor x + 1. Im 4. Nenner tritt dieser Faktor mit der höchsten Potenz auf, nämlich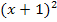 
. Daher muss 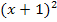ein Teil des Hauptnenners sein.
Weitere Faktoren gibt es hier nicht. Der Hauptnenner ist somit das Produkt von 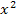und .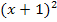
Der Hauptnenner ist daher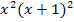 
.
Noch einmal alles kurz zusammengefasst. (Die höchsten Potenzen der einzelnen Faktoren sind farbig unterlegt. Das Produkt der höchsten Potenzen der auftretenden Faktoren ist der Hauptnenner.)
1. Nenner: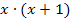
2. Nenner: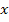
3. Nenner: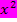 
4. Nenner: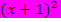 
Hauptnenner: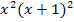
Hoffentlich hast du nachvollziehen können, wie man den Hauptnenner bestimmt hat. Wenn es dir noch nicht hundertprozentig klar geworden sein sollte, gehst du am besten in das Kapitel Bruchterme. Dort wird es bei der Addition und Subtraktion noch einmal ausführlich erklärt.
Jetzt aber wieder zu unserer Gleichung. Wir multiplizieren nun auf beiden Seiten mit dem Hauptnenner.
| 
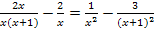
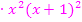
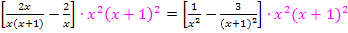
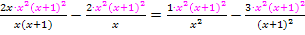
Wir kürzen und erhalten so:
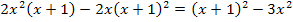
Diese Gleichung enthält kein x mehr im Nenner;sie kann leicht gelöst werden. Versuche es doch wirklich alleine, also ohne die folgende Lösung anzuschauen!
Aber Vorsicht bei dem Minus im Ausdruck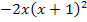 
, es bezieht sich auf den ganzen nachfolgenden Ausdruck.
Außerdem musst du beachten, dass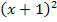 
nicht das Selbe ist wie 
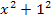. Warum das so ist und was richtig ist, wirst du bestimmt gleich verstehen:
Schüler, die noch keine Binomischen Formelngelernt haben, rechnen an Stelle von 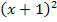einfach 
.
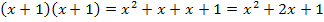Schüler, die die Binomischen Formeln im Unterricht bereits behandelt haben, können auch einfach die erste Binomische Formel verwenden:
Zur Erinnerung:
1. Binomische Formel: 
