Rechnerische Lösungsverfahren von Bruchgleichungen

2. Bsp.:

Ermittle die Lösungsmenge der folgenden Gleichungen!

a.)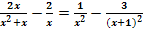       

b.)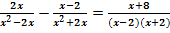       

c.)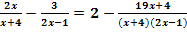        

d.)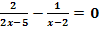       

Lösung:

zu a.)

Hier noch einmal die Gleichung: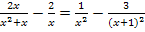       

Damit sich die Definitionsmenge besser erkennen lässt, klammern wir erst einmal soweit möglich aus. Man kann natürlich nur im Nenner des ersten Bruchs x ausklammern. Mehr geht nicht.

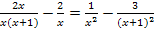
Jetzt lässt sich die Definitionsmenge leicht ablesen. Der Nenner des ersten Bruchs wird Null, wenn man x = 0 oder x = -1 einsetzt. Der Nenner des zweiten und dritten Bruchs ergibt nur dann Null, wenn man x = 0 einsetzt. Der Nenner des letzten Bruchs wird für x = -1 Null. Also dürfen für x die Zahlen -1 und 0 nicht eingesetzt werden. Die Definitionsmenge lautet daher:

D = ℚ 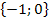bzw. ab der 9. Klasse: D = ℝ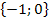

Jetzt lösen wir die Gleichung, indem wir mit dem Hauptnenner der gesamten Gleichung multiplizieren. Dazu brauchen wir erst ´mal den Hauptnenner. Da viele Schüler Probleme haben den Hauptnenner in schwierigeren Fällen selbst zu finden, soll im Folgenden eine Art Patentrezept zur Ermittlung des Hauptnenners gezeigt werden.

Hauptnenner ermitteln: Jeden Nenner soweit möglich faktorisieren, d.h. im Nenner ausklammern oder eventuell, wenn du das schon gelernt hast, Binomische Formeln oder Satz von Vieta anwenden. (Binomische Formeln und Satz von Vieta sind erst Stoff der 9. Klasse.) Die Faktoren jedes Nenners einzeln betrachten. Wenn Zahlen vorkommen:Jede Zahl in ihre Primfaktoren zerlegen, also als Produkt von Primzahlen schreiben. Nun schauen, bei welchem Nenner ein bestimmter Faktor am häufigsten vorkommt, also mit der höchsten Potenz. Mit dieser höchsten Potenz kommt der Faktor im Hauptnenner vor. Mit allen weiteren Faktoren entsprechend vorgehen. Der Hauptnenner ist dann das Produkt aus den höchsten Potenzen aller vorkommenden Faktoren bzw. Primfaktoren.

Jetzt wenden wir das auf unsere Aufgabe an.

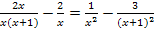
Jeder Nenner ist bereits vollständig faktorisiert, d.h. jeder Nenner ist als Produkt geschrieben. Ein Quadrat gilt dabei natürlich auch als Produkt, es ist ja bekanntlich 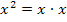bzw.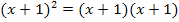

Wir schreiben uns zur Übersicht die Faktoren jedes einzelnen Nenners noch einmal auf. Das musst du nicht unbedingt machen. Eigentlich geht das auch im Kopf. Damit du aber die Überlegungen besser nachvollziehen kannst, ist hier alles ganz besonders ausführlich beschrieben.

---