Rechnerische Lösungsverfahren von Bruchgleichungen
| 
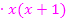
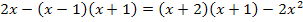
Diese Gleichung kennst du ja;das ist schließlich die Gleichung, die wir oben beim 1. Verfahren auch schon erhalten und dort auch schon gelöst haben. Noch einmal machen wir das jetzt nicht mehr. Schauen wir uns lieber die nächste Teilaufgabe an!
zu 1f.)
Hier noch einmal die Angabe: 
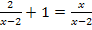
Lösung:
Definitionsmenge: D = ℚ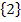 
Die linke Seite der Gleichung steht nicht auf einem einzigen Bruchstrich. Daher darf keinesfalls sofort kreuzweise multipliziert werden. Da auf beiden Seiten der Gleichung der selbe Nenner vorkommt, multiplizieren wir sofort alles mit dem Hauptnenner der gesamten Gleichung. Dieser Hauptnenner ist natürlich x – 2.
| 
| 
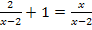
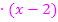
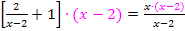
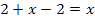
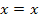
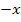
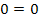
Ja, was ist denn das jetzt wieder? Wo ist denn das x abgeblieben? Jetzt überlege dir bitte erst einmal, was du selbst bei dieser Teilaufgabe als Lösungsmenge schreiben würdest.
Die Lösungsmenge ist hier eigentlich nicht wirklich gefragt. Es heißt ja in der Angabe nur:„Berechne die Lösungen …!“ Aber nicht etwa:„Gib die Lösungsmenge an!“ Das ist nämlich ein Unterschied. „Berechne die Lösungen …!“ bedeutet nur, dass nach x aufgelöst werden soll. „Gib die Lösungsmenge an!“ bedeutet dagegen, dass nach x aufgelöst und zusätzlich die Lösungsmenge angegeben werden muss. Bei dieser Fragestellung gibt es einen Extrapunkt auf die Angabe der Lösungsmenge bzw. einen Punkt abgezogen, wenn man die Lösungsmenge nicht angibt.
Auch wenn es hier nicht verlangt ist:Was ist denn hier die Lösungsmenge?
Bist du der Meinung, dass L =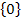 
stimmt?
Ist das wirklich richtig?
An Hand der Fragestellung, weißt du natürlich schon, dass L = 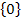falsch ist. Aber warum? Und was ist denn dann die richtige Lösungsmenge?
Am Ende der Rechnung ergab sich 0 = 0. Das ist eine wahre Aussage. Das bedeutet, dass die Aussage immer wahr ist, egal was man für x einsetzt. Für jedes beliebige x scheint die Gleichung erfüllt zu sein, denn 0 = 0 ist ja immer wahr. Aber Vorsicht:Denke an die Definitionsmenge D = ℚ 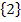! Für x darf die Zahl 2 nicht eingesetzt werden, da sonst der Nenner Null werden würde. D.h. für jedes beliebige x aus der Definitionsmenge ist die Gleichung erfüllt. Die Lösungsmenge entspricht daher der Definitionsmenge:
L = D = ℚ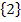
Konkret lässt sich hier die Lösung also gar nicht angeben;es gibt eben unendlich viele Lösungen. x kann alles sein bloßnicht 2.
| Merke:
Für Bruchgleichungen, bei denen sich am Ende der Rechnung x komplett heraushebt und dann eine wahre Aussage (z.B.:0 = 0) entsteht, gilt immer:L = D Wahre Aussage |
Für Bruchgleichungen, bei denen sich am Ende der Rechnung x komplett heraushebt und dann eine falsche Aussage (z.B.:2 = 5) entsteht, gilt immer:L = 
Falsche Aussage |
Für den Fall, dass sich eine wahre Aussage am Ende der Rechnung ergibt, haben wir ja gerade ein Beispiel gesehen. Allerdings noch nicht für den anderen Fall, dass am Schluss der Rechnung ein Widerspruch entsteht. Also schauen wir gleich ´mal ein neues Beispiel an, wobei auch dieser Fall auftritt. Zwei der nächsten vier Teilaufgaben führen jeweils zu einem Widerspruch, also wird bei diesen Aufgabe die Lösungsmenge leer sein. Welche sind es? Das sieht man natürlich nicht sofort. Du musst schon rechnen. Also gleich selbst probieren!
