Rechnerische Lösungsverfahren von Bruchgleichungen
Hättest du fälschlich x + 1 für den Hautnenner gehalten, würdest du im Folgenden die gesamte Gleichung auf beiden Seiten nur mit x + 1 an Stelle des richtigen Hauptnenners x(x + 1) multiplizieren. Dann würde sich das x im Nenner des zweiten und dritten Bruchs nicht weg kürzen lassen. Die Multiplikation mit dem Faktor x + 1 würde also nicht dazu führen, dass alle x im Nenner wegfallen. Damit du das besser verstehst, machen wir das trotzdem einmal, obwohl es uns natürlich nicht zur Lösung führt. x + 1 ist ja nicht der Hauptnenner und daher bringt die Multiplikation mit x + 1 einfach nichts! Aber genau das sollst du eben daran lernen.
| 
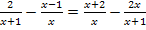
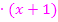(Das ist nicht der Hauptnenner!)
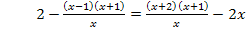
Du siehst, dass sich eine Gleichung ergibt, die x immer noch im Nenner enthält, und deshalb hat uns die Multiplikation mit dem Faktor x + 1 nicht weiter gebracht. x + 1 ist eben nicht der Hauptnenner! Nur die Multiplikation mit dem Hauptnenner führt zu einer Gleichung ohne x im Nenner, die sich dann leicht lösen lässt. Sollte bei dir also irgendwann einmal das x nicht aus allen Nennern heraus gekürzt werden können, dann hast du nicht mit dem Hauptnenner multipliziert. Du hast also vermutlich einen Fehler bei der Ermittlung des Hauptnenners gemacht.
Jetzt wollen wir uns aber endlich den richtigen Lösungsweg der Gleichung ansehen. Wir multiplizieren mit dem korrekten Hauptnenner der ganzen Gleichung, also mit x(x + 1).
| 
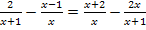
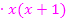(Das ist der Hauptnenner!)
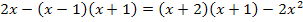
Rechne diese Gleichung bitte erst einmal alleine aus, bevor du weiter liest! Zumindest den nächsten Schritt bitte wirklich selbst ausrechnen und aufschreiben. Weiterrechnen musst du noch gar nicht unbedingt.
Hast du den nächsten Schritt wirklich alleine gerechnet? Wenn nicht, dann jetzt!!!
