Rechnerische Lösungsverfahren von Bruchgleichungen

Nun kannst du alle drei Lösungswege direkt miteinander vergleichen und dir die Methode heraussuchen, die deiner Meinung nach am einfachsten ist. (Siehe dazu die direkte Gegenüberstellung der drei Verfahren!) Vermutlich wirst du dich für das kreuzweise Multiplizieren entscheiden, denn das ist bei dieser Aufgabe wohl der schnellste Lösungsweg.

Übersicht über die drei Lösungswege:

Vorab wurde die Gleichung 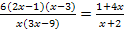gekürzt, so dass  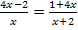  entstand. Außerdem wurde die Definitionsmenge D = ℚ 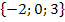ermittelt.

Nun gehen wir von der gekürzten Form der Gleichung aus. Um die Gleichung nach x aufzulösen, stehen die drei folgenden Möglichkeiten zur Verfügung:

Danach muss überprüft werden, ob der berechnete Wert in der Definitionsmenge liegt. Das ist der Fall. Deshalb macht man noch die Probe. Fertig!

Nun aber zur nächsten Teilaufgabe.

zu 1e.)

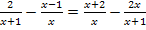
Lösung:

Als erstes geben wir die Definitionsmenge an;sie lässt sich ja leicht ablesen:  D = ℚ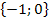

Weder auf der linken noch auf der rechten Seite der Gleichung steht ein einzelner Bruch, sondern jeweils eine Differenz aus zwei Brüchen. Die Gleichung hat also nicht die Form 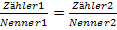und daher dürfen wir hier nicht einfach kreuzweise multiplizieren. Wir müssen die beiden Brüche, die sich jeweils auf der selben Seite der Gleichung befinden, erst auf einen gemeinsamen Nenner bringen, damit wir kreuzweise multiplizieren dürfen. Das ist jedoch ziemlich aufwendig. Also nehmen wir lieber das 1. Verfahren und multiplizieren sofort mit dem Hauptnenner der Gleichung.

1. Vefahren:Mit dem Hauptnenner multiplizieren und kürzen

Bevor wir damit beginnen können, müssen wir uns natürlich den Hauptnenner überlegen. Das ist hier nicht schwer;du kannst das sicher alleine. Also überlege ihn dir ´mal selbst!

Hoffentlich bist du darauf gekommen, dass der Hauptnenner hier x(x + 1) ist.

Solltest du jedoch gedacht haben, dass der Hauptnenner x + 1 ist, was natürlich falsch ist, überlege dir Folgendes:Der Hauptnenner ist doch der Nenner, auf den sich alle in der Gleichung vorkommenden Brüche erweitern lassen könnten. Erweitern kann man nur durch Multiplizieren, jedoch nicht durch + oder  -  rechnen. Wie soll man dann aber die Brüche 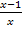und 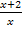auf den Nenner x+ 1 bringen? Das geht eben nicht! Deshalb kann x + 1 alleine nicht der Hauptnenner sein.

---