Rechnerische Lösungsverfahren von Bruchgleichungen
Da es sich hier um eine Bruchgleichung der Form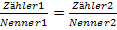 
handelt, also um eine Gleichung, bei der auf beiden Seiten ein einzelner Bruch vorliegt, können wir unser 2. Verfahren, das kreuzweise Multiplizieren, anwenden.
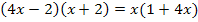
Jetzt müssen wir nur noch ausmultiplizieren und nach x auflösen. Das ist ja nicht mehr schwer.
Nun erkennst du, dass auf beiden Seiten der Term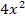 
vorkommt. Nach der Subtraktion von 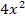auf beiden Seiten der Gleichung fällt 
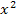vollständig heraus. In der 8. Klasse brauchst du nur Gleichungen lösen können, bei denen dies der Fall ist.
| 
| 
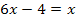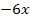
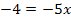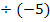
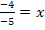
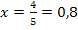
Der berechnete Wert liegt in der Definitionsmenge D = ℚ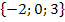 
. Der Wert 0,8 ist schließlich keine der Definitionslücken -2, 0 oder 3.
Wir machen noch schnell die Probe:
Hier noch einmal die Gleichung: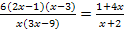 
Probe für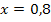 
: 
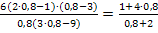
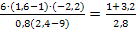
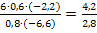
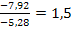
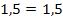(wahr)
Somit ist die Lösung tatsächlich: 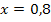Fertig!
Nur zum Vergleich:Diese Teilaufgabe noch einmal aber mit dem 1. Verfahren gelöst. Dass dies hier allerdings nicht so praktisch ist, wirst du gleich selber sehen.
Hier noch einmal die Angabe:
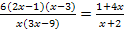
Ausgeklammert und gekürzt haben wir oben schon:
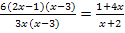
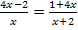
Die Definitionsmenge haben wir ebenfalls oben schon ermittelt: D = ℚ
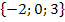
Wir gehen nun von der gekürzten Form aus:
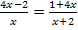
Der Hauptnenner ist hier natürlich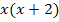 
. Daher multiplizieren wir jetzt auf beiden Seiten mit 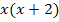. Dann kürzen wir.
| 
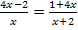
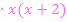
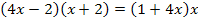
Das ist wieder die selbe Gleichung, die wir schon beim kreuzweise Multiplizieren erhalten haben. Ab hier ist der Rechenweg identisch mit dem schon oben gezeigten Lösungsweg. Daher wird er nicht noch einmal gezeigt. Auf jeden Fall konntest du sehen, dass es so auch geklappt hätte. Es dauert halt nur etwas länger und ist auch etwas schwieriger.
Das dritte Verfahren funktioniert natürlich ebenfalls. Schauen wir uns das auch noch an:
Hier noch einmal die Angabe:
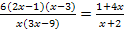
Ausgeklammert und gekürzt haben wir oben schon:
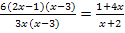
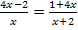
Die Definitionsmenge übernehmen wir wieder von oben: D = ℚ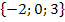
Wir gehen nun von der gekürzten Form aus:
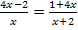
Der Hauptnenner ist hier natürlich 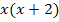. Jetzt müssen wir die beiden Brüche jeweils so erweitern, dass sie beide den Nenner 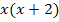haben. Der linke Bruch muss daher mit 
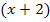und der rechte Bruch mit x erweitert werden.
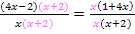
Jetzt lassen wir den gemeinsamen Nenner einfach weg. (Das entspricht praktisch dem Multiplizieren mit dem Hauptnenner mit nachfolgendem Kürzen.) Wir setzen also nur noch die Zähler gleich:
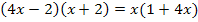
Das ist natürlich wieder die selbe Gleichung, die wir schon zweimal erhalten haben:Einmal durch das sofortige Multiplizieren der gekürzten Gleichung mit dem Hauptnenner und ein weiteres Mal durch das kreuzweise Multiplizieren. Ab hier geht es wieder so weiter, wie schon beim kreuzweisen Multiplizieren gezeigt.
