Anwendungsaufgaben zum Thema Bruchgleichungen

Wenn man die Eier zusammen kocht, ändert das ja nichts an der Kochzeit! Es geht ja deshalb nicht etwa schneller, bloßweil man zwei Eier gemeinsam kocht. Das kleine Ei wird immer noch nach 5 Minuten wachsweich sein und das große Ei nach 6 Minuten, egal ob sie alleine oder gemeinsam gekocht werden. Vermutlich würde man einfach das kleine Ei 1 Minute früher aus dem Kochwasser nehmen, wenn man die beiden Eier gemeinsam kochen wollte.

Hier gibt es also gar nichts zu rechnen!

Wenn ich dich tatsächlich auf´s Glatteis führen und dich zum Rechnen verführen konnte, bitte nicht sauer auf mich oder gar traurig sein. Es war nicht böse gemeint. Ehrlich gesagt, zielte diese Aufgabe einzig und allein darauf ab, dich hinters Licht zu führen. Aber einzig aus dem Grund, dass dich dein Lehrer in einer Prüfung nicht mehr hereinlegen kann. Wenn du es aber selbst gemerkt hast, dass es hier nichts zu rechnen gab, kannst du stolz auf dich sein! Gut mitgedacht!

Dieses Beispiel sollte dir nur vorführen, dass man nicht immer stur nach dem Prinzip der Röhrenaufgaben vorgehen kann, bloßweil sich der Text so ähnlich anhört. Also bitte immer erst darüber nachdenken, ob es gemeinsam überhaupt schneller geht.

Jetzt aber wirklich wieder etwas zum Rechnen:

4. Bsp.: Die Linsengleichung

Die Optik ist ein Teilgebiet der Physik. Eine wichtige Formel in der Optik ist die sogenannte Linsengleichung. Für Sammellinsen (Linsen, die das Licht bündeln) gilt folgende Gleichung:

g: Gegenstandsweite (= Abstand des abgebildeten Gegenstands zur Linsenachse)

b: Bildweite (= Abstand des Bildes von der Linsenachse)

f: Brennweite der Linse (= Konstante, die von der Linse abhängt:Sie gibt jeweils den Abstand der beiden Brennpunkte von der Linsenachse an.)

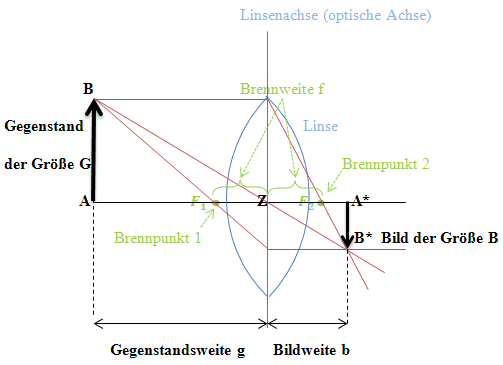
Am besten wird es sein, wenn du dir erst einmal die folgende Abbildung anschaust. Dann wird dir sicher gleich klar, was mit den Bezeichnungen g, b und f gemeint ist.

Abb.:Mittels einer Sammellinse der Brennweite f wird ein Gegenstand der Länge G = auf sein Bild mit der Länge B abgebildet. Hat der Gegenstand zur Linsenachse den Abstand g = , so erscheint das Bild im Abstand b = absolut scharf. Dann ist die Linsengleichung erfüllt.

---