Substitution
Manch komplizierte Gleichung lässt sich durch das Einführen einer neuen Lösungsvariable stark vereinfachen und somit auf eine gemischtquadratische Gleichung zurückführen. Dieses Verfahren nennt man Substitution (Lat. substituere = ersetzen).
9. Bsp.:
Berechne die Lösungen der folgenden Gleichung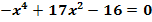 
.
Lösung:
Es handelt sich hier um eine Gleichung vierten Grades, weil die höchste Potenz von x vier ist. Das Besondere an dieser Gleichung ist, dass sie nur gerade Potenzen von x enthält. Es handelt sich um eine Gleichung der Form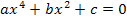 
. Solche Gleichungen nennt man biquadratische Gleichungen. Woher diese Bezeichnung kommt, wird klar, wenn man sich Folgendes überlegt:An Stelle von 
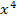kann man auch 
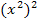schreiben, denn es gilt:
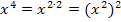
(Bei der letzten Umformung wurde das Potenzgesetz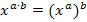 
verwendet.) Somit lässt sich eine Gleichung der Form 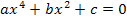auch als 
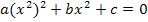schreiben. Jetzt erkennt man, dass hier die Unbekannte x gleich zweimal hintereinander quadriert vorkommt. Daher kommt wohl auch die Bezeichnung „biquadratisch“ (Lat. bis = zweimal).
Eine biquadratische Gleichung kann mit Hilfe eines kleinen Tricks ganz gut gelöst werden. Man führt eine Substitution durch. Man führt, wie oben schon erwähnt, eine neue Variable – nennen wir sie ´mal u – an Stelle von x in die Gleichung ein. Wir schreiben an Stelle von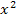 
die neue Variable u und an Stelle von 
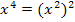entsprechend 
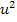. (Der Buchstabe u ist beliebig gewählt;man hätte jeden anderen Buchstaben außer x verwenden können.) Dadurch lässt sich nämlich eine biquadratische Gleichung mit der Variablen x in eine gemischtquadratische Gleichung mit der Variablen u umformen. Dann kann die Mitternachtsformel angewendet und zuerst einmal die neue Variable u bequem berechnet werden. Durch eine sogenannte Rücksubstitution kann letztendlich die ursprüngliche Variable x ermittelt werden. Genug der Worte, schauen wir uns einfach an, wie die Lösung mittels Substitution geht.
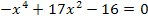
Substitution: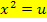 
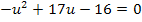
(Gemischtquadratische Gleichung mit der neuen Variablen u)
