Winkelhalbierende

Winkelhalbierende eines gegebenen Winkels:

Die Winkelhalbierende eines gegebenen Winkels 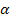ist, wie der Name schon sagt, diejenige Gerade, welche den Winkel 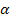halbiert. Siehe folgende Abbildung! Sie wird mit 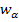bezeichnet.

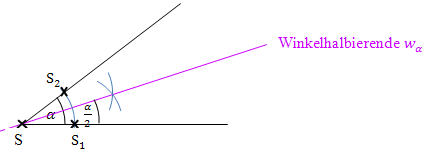
Abb.:Winkel mit seiner Winkelhalbierenden und Konstruktionslinien (blau), die schwarzen Kreuze stellen die Mittelpunkte der Kreisbögen bei der Konstruktion dar.

Konstruktion der Winkelhalbierenden Die Winkelhalbierende eines gegebenen Winkels wird folgendermaßen konstruiert: ·         Kreisbogen mit Mittelpunkt S (= Scheitel des Winkels) und beliebigem Radius zeichnen, um den Kreisbogen mit den Schenkeln des Winkels zu schneiden Schnittpunkte und ·         Die Punkte und sind die Mittelpunkte zweier weiterer Kreisbögen mit jeweils gleichem Radius. ·         Die Winkelhalbierende verläuft durch den Scheitel und den Schnittpunkt der zuletzt gezeichneten beiden Kreisbögen.

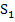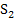Einfacher gesagt:Mit dem Zirkel im Scheitel S des Winkels einstechen;den Radius kannst du beliebig wählen, z.B. 3 cm. Dann zeichnest du den Teil des Kreises, der ein wenig über die Schenkel des Winkels hinausragt. Vergleiche Abb. oben! Wo der gezeichnete Bogen jeweils die beiden Schenkel schneidet, sind die Punkte und . In 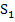mit dem Zirkel einstechen mit beliebigem Radius;am besten gleich den selben Radius nehmen wie schon vorher, dann musst du den Zirkel nicht verstellen. Dann einen Teil des Kreises zwischen den Schenkeln des Winkels zeichnen. Das Gleiche noch einmal nur mit 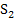als Mittelpunkt. Achtung:Jetzt darf der Radius nicht mehr verändert werden! Also noch einen Kreisbogen zeichnen, nun mit 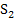als Mittelpunkt und dem gleichen Radius wie schon bei dem Kreisbogen mit 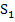als Mittelpunkt. Durch den Schnittpunkt der zuletzt gezeichneten zwei Kreisbögen und durch den Scheitel S des Winkels eine Gerade zeichnen;das ist die Winkelhalbierende des Winkels.

Die Punkte, die auf der Winkelhalbierenden liegen, haben jeweils den gleichen Abstand zu beiden Schenkeln des Winkels.

Winkelhalbierenden zweier Geraden:

Wenn zwei Geraden g und h gegeben sind, die sich im Punkt S schneiden, gibt es zwei Winkelhalbierenden 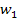und 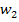, das sogenannte Winkelhalbierendenpaar. Die eine halbiert den spitzen Winkel, die andere den stumpfen. Die beiden Winkelhalbierenden stehen immer aufeinander senkrecht. Die Konstruktion geht jeweils nach dem selben Prinzip wie bei einem Winkel.

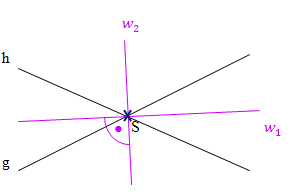
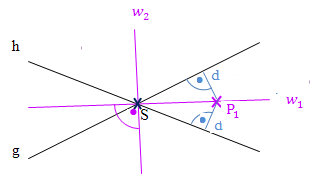
Abb.:Geraden g und h mit den beiden Winkelhalbierenden 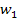und 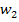(lila)

Winkelhalbierendenpaar als geometrischer Ort:

Das Winkelhalbierendenpaar bildet den geometrischen Ort der Punkte mit jeweils gleichem Abstand zu beiden Geraden g und h, d.h. die Menge aller Punkte, welche von den beiden Geraden g und h jeweils die gleiche Entfernung haben. Jeder beliebige Punkt einer der beiden Winkelhalbierenden ist somit von der Gerade g genauso weit entfernt wie von der Gerade h. Betrachte dazu die folgende Abbildung! Der Punkt 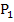ist ein beliebiger Punkt auf einer der beiden Winkelhalbierenden. Er dient hier nur als Beispiel. (Man hätte statt 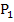auch irgendeinen anderen Punkt auf 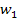oder 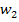nehmen können.) 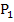hat zur Gerade g den gleichen Abstand d wie zur Geraden h.

Für Schüler der gymnasialen Oberstufe:

Gleichungen der Winkelhalbierenden in der analytischen Geometrie:

Wenn zwei sich schneidende Geraden in ihrer Parameterform, also mit Aufpunkt und Richtungsvektor, gegeben sind, können leicht die Gleichungen der beiden Winkelhalbierenden 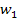und 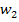in Parameterform aufgestellt werden.

Geg.:

Die beiden Geraden schneiden sich im Punkt S.

Ges.:Gleichungen der Winkelhalbierenden 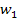und 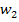in Parameterform

Der Schnittpunkt S der beiden Geraden kann jeweils als Aufpunkt der Winkelhalbierenden verwendet werden. Als Richtungsvektoren der Winkelhalbierenden nimmt man jeweils einen der beiden Winkelhalbierendenvektoren 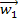und 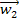der zwei Richtungsvektoren 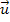und 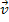. Der Winkelhalbierendenvektor 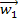ist der Vektor, welcher den Winkel zwischen den Richtungsvektoren 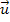und 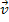halbiert. 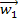oder ein Vielfaches davon wird als Richtungsvektor der Winkelhalbierenden 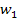verwendet. Der Vektor 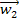halbiert den Nebenwinkel der zwei Richtungsvektoren 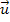und 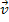. 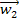oder ein Vielfaches von 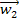kann somit als Richtungsvektor der Winkelhalbierenden 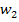verwendet werden. Vergleiche dazu die folgende Abbildung!

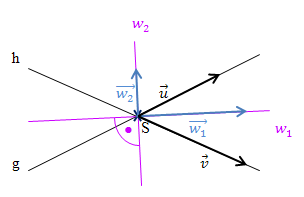
Abb.:Zwei Geraden  g und h mit ihren Winkelhalbierenden 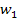und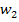

Die beiden Winkelhalbierendenvektoren 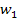und 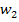können mit Hilfe der Einheitsvektoren 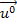und 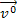berechnet werden.

---