Wendetangente
Unter einer Wendetangente versteht man die Tangente an einen Funktionsgraph 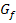 im Wendepunkt W der Funktion
im Wendepunkt W der Funktion 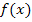 . Die Gleichung der Wendetangente wird im Prinzip genauso berechnet wie jede andere Tangente an
. Die Gleichung der Wendetangente wird im Prinzip genauso berechnet wie jede andere Tangente an 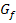 in einem beliebigen, gegebenen Kurvenpunkt P. Man verwendet an Stelle des gegebenen Kurvenpunktes P einfach den Wendepunkt W, den man natürlich vorher berechnen muss.
in einem beliebigen, gegebenen Kurvenpunkt P. Man verwendet an Stelle des gegebenen Kurvenpunktes P einfach den Wendepunkt W, den man natürlich vorher berechnen muss.
Geg.:Funktionsgleichung 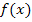
Wendepunkt berechnen: 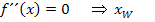
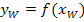
In Worten:Man findet die x-Koordinate 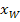 des Wendepunkts, indem man die zweite Ableitung
des Wendepunkts, indem man die zweite Ableitung 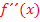 gleich Null setzt und nach x auflöst. Dann die berechnete x-Koordinate in die Funktionsgleichung
gleich Null setzt und nach x auflöst. Dann die berechnete x-Koordinate in die Funktionsgleichung 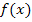 einsetzten, um die y-Koordinate
einsetzten, um die y-Koordinate 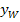 des Wendepunkts zu berechnen. Jetzt kennst du die Koordinaten des Wendepunktes
des Wendepunkts zu berechnen. Jetzt kennst du die Koordinaten des Wendepunktes 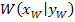 .
.
Nachweisen, dass es sich wirklich um einen Wendepunkt handelt:
1. Möglichkeit:Mit Hilfe des Krümmungsverhaltens von 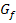 .
.
Zeigen, dass sich tatsächlich das Vorzeichen der zweiten Ableitung an der Stelle 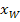 ändert.
ändert.
2. Möglichkeit:Mit der dritten Ableitung
x-Koordinate 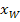 in die dritte Ableitung einsetzen und zeigen, dass das Ergebnis ungleich Null ist. (Näheres dazu bei Wendepunkte mit dritter Ableitung
in die dritte Ableitung einsetzen und zeigen, dass das Ergebnis ungleich Null ist. (Näheres dazu bei Wendepunkte mit dritter Ableitung 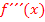 nachweisen)
nachweisen)
| Anleitung zum Aufstellen der Gleichung einer Wendetangente:
Vorweg berechnet wurden die Koordinaten des Wendepunkts · Allgemeiner Ansatz: · D.h. du sollst die x-Koordinate des Wendepunktes in die erste Ableitung · Setze in den allgemeinen Ansatz · Setze die berechneten Werte für m und t in |
Wozu braucht man die Wendetangente?
Man kann den Graph der Funktion wesentlich genauer zeichnen, wenn man die Gleichung der Wendetangente(n) kennt. Man zeichnet zuerst den Wendepunkt mit zugehöriger Wendetangente und eventuell vorhandene Nullstellen, Extrema und Asymptoten in ein Koordinatensystem. Der Graph kommt von der einen Seite an die Wendetangente heran, ändert im Wendepunkt seine Krümmung und geht dann wieder von der anderen Seite weg von der Wendetangente. Vergleiche Abbildung unten! Somit kann man den Graph wesentlich genauer zeichnen, wenn man die Wendetangente kennt. Sie wird oft in Prüfungen verlangt, auch im Abitur!
Im Wendepunkt verläuft der Graph lokal am steilsten oder flachsten. Die Steigung der Wendetangente ist daher lokal die größte bzw. kleinste Steigung der Funktion.
Hat eine Funktion mehrere Wendepunkte, gibt es natürlich auch mehrere Wendetangenten. Sie müssen einzeln berechnet werden.
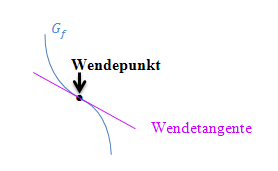
Abb.:Funktionsgraph mit Wendepunkt und Wendetangente
Ein Wendepunkt mit waagrechter Tangente wird als Terrassenpunkt bezeichnet. Ein Terrassenpunkt ist somit ein Sonderfall des Wendepunktes. Die Steigung im Terrassenpunkt ist gleich Null.

Abb.:Funktionsgraph mit Terrassenpunkt und waagrechter Wendetangente
Konkrete Aufgabenbeispiele zur Berechnung von Wendepunkt und Wendetangente findest du im Bereich Analysis bei zweite Ableitung 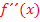 .
.


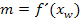
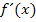 einsetzen;das ergibt die Steigung m der Wendetangente.
einsetzen;das ergibt die Steigung m der Wendetangente.