Wendepunkt

Unter einem Wendepunkt einer Funktion, kurz WEP oder WP genannt, versteht man einen Punkt auf dem Funktionsgraph, in dem sich das Krümmungsverhalten der Funktion ändert. Am besten erkennst du einen Wendepunkt auf einem gegebenen Funktionsgraph folgendermaßen:Stell dir vor, du würdest beispielsweise mit einem Fahrrad auf dem Graph entlang fahren. An der Stelle, wo du von rechts nach links oder umgekehrt umlenkst, befindet sich ein Wendepunkt. Eine Funktion kann natürlich auch mehrere verschiedene Wendepunkte besitzen.

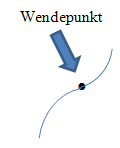
Ein Wendepunkt mit waagrechter Tangente heißt Terrassenpunkt.

Rechnerisch ermittelt man die x-Koordinaten der Wendepunkte, indem man die zweite Ableitung f´´(x) gleich Null setzt.

Wendepunkt:  f´´(x) = 0

Die y-Koordinaten erhält man, wenn man die gerade ermittelten x-Koordinaten jeweils in den Funktionsterm f(x) einsetzt. Allerdings ist jetzt noch nicht sicher, dass die ermittelten Punkte wirklich Wendepunkte sind. Es könnten auch nur sogenannte Flachpunkte sein. In einem Flachpunkt ist zwar die Krümmung f´´(x) gleich Null, aber es braucht sich dort das Krümmungsverhalten nicht zu ändern. Um zu beweisen, dass ein Wendepunkt vorliegt, muss daher zusätzlich noch gezeigt werden, dass sich das Vorzeichen der zweiten Ableitung f´´(x) an dieser Stelle wirklich ändert.

Der Vorzeichenwechsel von f´´(x) am Wendepunkt kann beispielweise mit Hilfe einer Krümmungstabelle gezeigt werden. Siehe dazu auch:Krümmung/Krümmungsverhalten

Eine andere Methode zum Nachweis eines Wendepunkts verwendet die dritte Ableitung f´´´(x). Man braucht nur die x-Koordinate des (vermutlichen) Wendepunkts 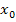in die dritte Ableitung einsetzen. Ergibt sich dabei eine Zahl ungleich Null, liegt sicher ein Wendepunkt vor.

f´´´( 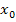) 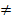0

Mehr zu diesem Thema im Bereich Analysis in den Kapiteln Zweite Ableitung f´´(x) und Kurvendiskussion.